反比例と円のグラフを習得する【電気数学のすゝめ21】

電験取得のための第一歩

2025.12.26

21限目
反比例、円のグラフ

先生　前回は二次関数の性質とグラフの描き方について学習したよね。
生徒　はい。グラフを描くことで二次方程式の解が2つあることを確認しました。
先生　うん、しっかりマスターしているみたいだね。それでは、今回のテーマだ。まずは反比例について学ぼう。
生徒　はい。

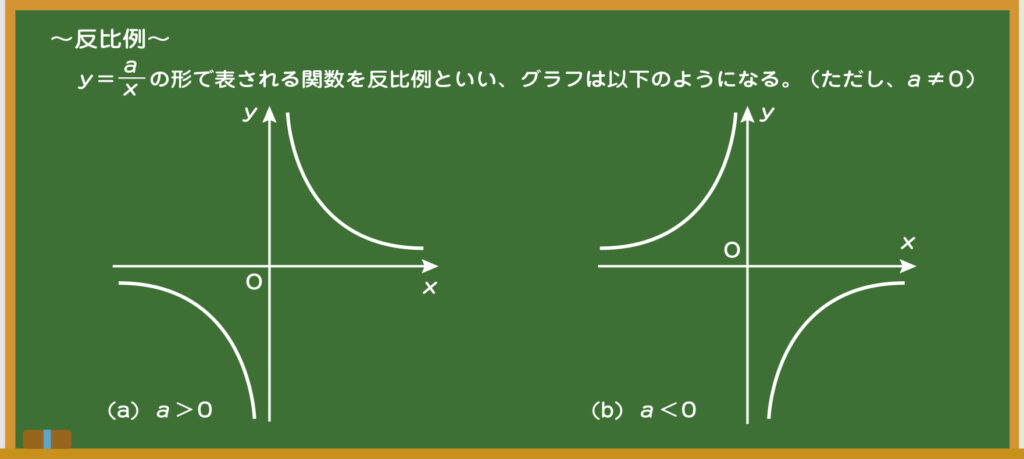
先生　黒板の図が反比例のグラフだよ。何か気がつくことはあるかな？
生徒　グラフが2つに分かれていますね。
先生　うん、いいところに気がついたね。反比例は「双曲線」というグラフの特別な場合なんだ。双曲線という名前のとおり、2つの曲線で描かれているね。もう1点、気がついてほしいことがあるんだけど、どうかな？
生徒　う～ん。
先生　それでは、質問ね。反比例のグラフはx軸、y軸と接触するか、しないか？
生徒　黒板の図をみる限りは接触していない……。
先生　そう、正解！　よくチェックしているね。「接触しない」だ。厳密には「限りなく近づく」という表現になるんだ。数学の分野では「極限」というテーマで扱っているよ。
生徒　電気と関係あるんですか？
先生　もちろんだよ。例えば、真空中に置かれた点電荷による電位Vと点電荷からの距離rとの関係は「V= $\frac{Q}{4 {π ε}_{0} r}$ 」と表すことができるよね。電荷Qを一定として「a= $\frac{Q}{4 {π ε}_{0}}$ 」とすると「V= $\frac{a}{r}$ 」と反比例の式になる。
生徒　あっ、ホントだ！
先生　したがって、距離rと電位Vのグラフは図1のように描けるんだ。ここで、電位Vが0となる距離rについて考えてみよう。まず、距離rがどうなれば、電位Vは小さくなるかな？

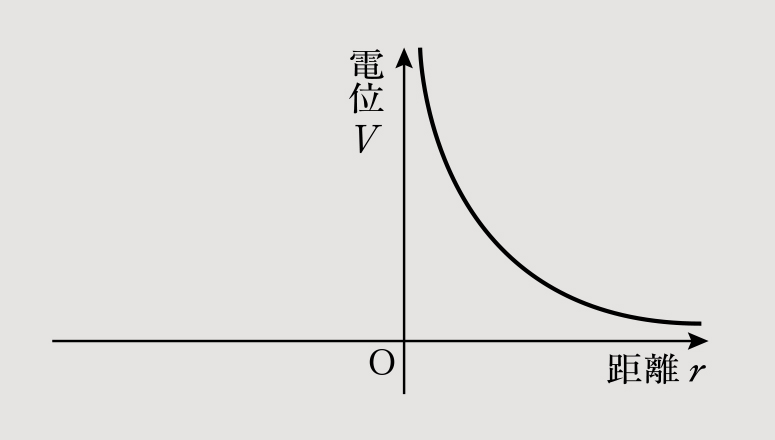
生徒　距離rが大きくなれば、電位Vは小さくなります。
先生　そうだね。それでは、電圧Vが0になる距離rの大きさは？
生徒　う～ん。距離rが大きくなればなるほど、電位Vは0に近づいて……。
先生　うまく表現できないでしょう。この問題に「極限」の考え方を用いれば「距離rが限りなく無限大に近づくとき、電位Vは0に収束する」と表現するんだ。
生徒　数学に無限大なんて使っていいんですか？
先生　もちろん。無限大を表す記号「∞」もあるからね。ちゃんと定義されているよ。
生徒　へぇ～。
先生　話を電位に戻すと、電位が0になる点は距離が無限大に離れたところであるという結論になる。この無限大に離れた点のことを「無限遠点」と呼ぶんだ。電気を学習していると、いずれ登場するから覚えておくといいよ。
生徒　無限遠点って、どこにあるんですか？
先生　う～ん。限りなく遠いところであると思っておけばいいよ。
生徒　は～い。

練習問題
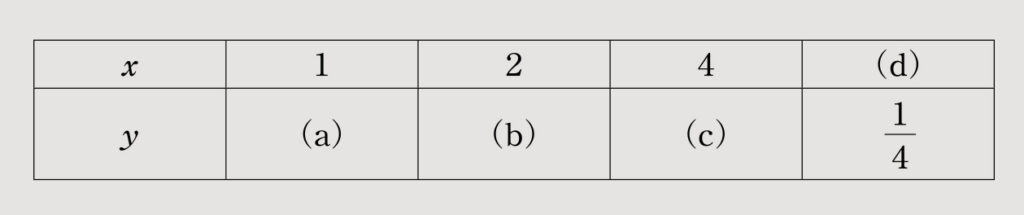
（1）次の表の値は関数y= $\frac{2}{x}$ のものである。（a）～（d）の値を求めなさい。

（2）y= $\frac{1}{x}$ のグラフを描きなさい。
（3）y= $\frac{4}{x}$ のグラフを描きなさい。

答
（1）y＝ $\frac{2}{x}$ に、それぞれx、yの値を代入して求める。
（a）y＝ $\frac{2}{x}$ にx＝1を代入すると、y＝ $\frac{2}{1}$ ＝2
（b）y＝ $\frac{2}{x}$ にx＝2を代入すると、y＝ $\frac{2}{2}$ ＝1
（c）y＝ $\frac{2}{x}$ にx＝4を代入すると、y＝ $\frac{2}{4}$ ＝ $\frac{1}{2}$
（d）y＝ $\frac{2}{x}$ にy＝ $\frac{1}{4}$ を代入すると、 $\frac{1}{4}$ ＝ $\frac{2}{x}$ 、x＝2×4＝8

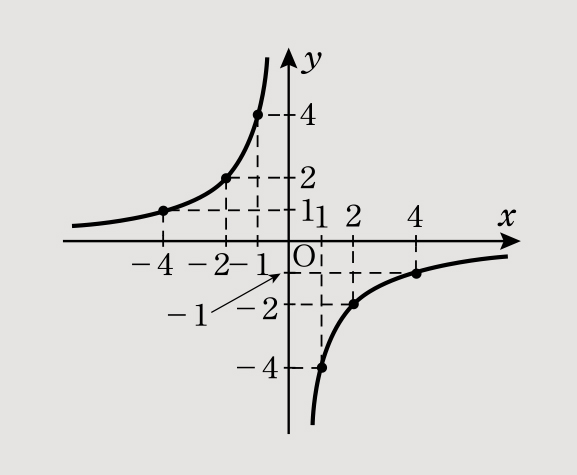
（2）y＝ $\frac{1}{x}$ のグラフは以下となる。

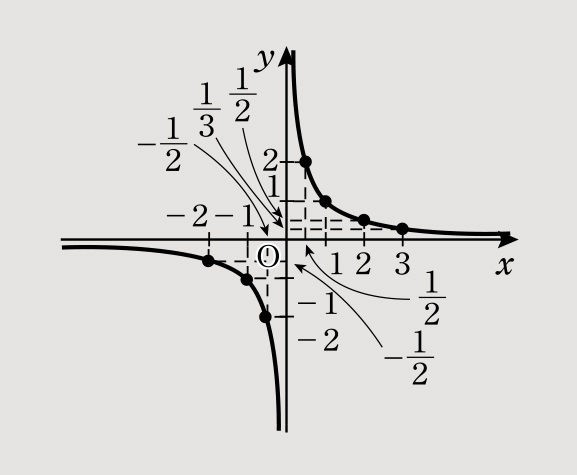
（3）y＝－ $\frac{4}{x}$ のグラフは以下となる。

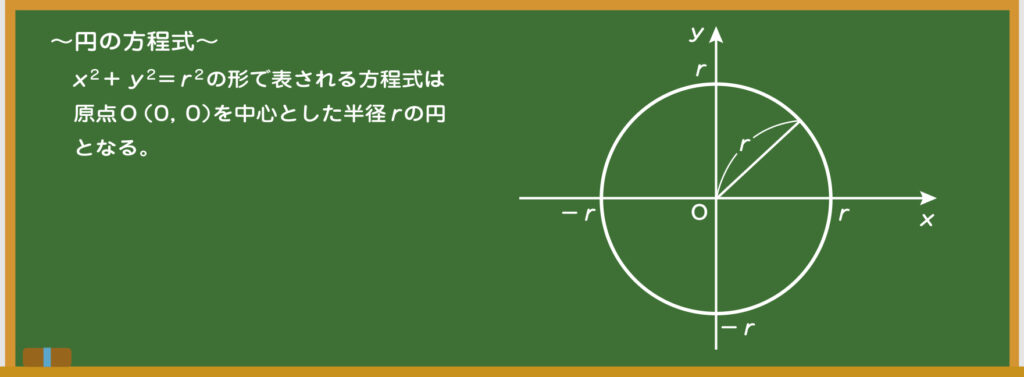
先生　さて、次は円のグラフに取り組もう。黒板にあるように「x²＋y²＝r²」のグラフを描くと円になるんだ。
生徒　なぜ、この式が円になるんですか？
先生　いい質問だね。円というのは中心からの距離が等しい点の集まりだ（図2）。つまり、円周上の点と円の中心の距離は必ず半径rになるよね。
生徒　はい。
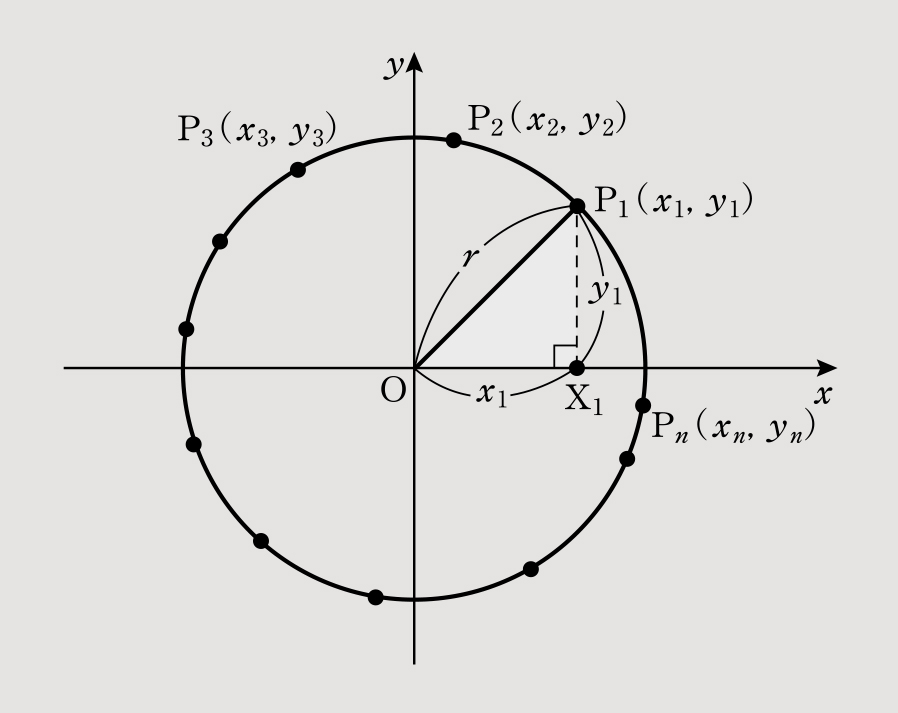
先生　これを数式で表してみよう。円周上の点を点P₁（x₁,y₁）として、円の中心O（0,0）との距離OP₁をx₁、y₁で表すと、どうなるかな？
生徒　う～ん。
先生　ヒントね。三角形OP₁X₁は直角三角形だから、三平方の定理が……。
生徒　あっ、x₁²＋y₁²＝r²です！
先生　うん、正解。もう円の方程式の形がみえているよ。この関係は円周上の点であれば、どこでも成り立つから「点P₂：x₂²＋y₂²＝r²」「点P₃：x₃²＋y₃²＝r²」……「点P_n：x_n²＋y_n²＝r²」となるよね。したがって、円の方程式は「x²＋y²＝r²」となるんだ。
生徒　なんとなくですけど、わかりました。
先生　いまは「x²＋y²＝r²」が円の方程式であることがわかれば十分だよ。それじゃあ、練習問題に取り組んでみようか。

練習問題
　次の式は円の方程式である。これらの円の半径を求めよ。
（1）x²＋y²＝2²
（2）x²＋y²＝25
（3）x²＋y²＝3
（4）x²＋y²－5＝0

答
円の方程式はx²＋y²＝r²であるから、それぞれの式と比較して半径rを求める。
（1）式から、半径2の円となる。
（2）「x²＋y²＝25、x²＋y²＝5²」となり、半径5の円となる。
（3）「x²＋y²＝3、x²＋y²＝（√3）²」となり、半径√3の円となる。
（4）「x²＋y²－5＝0、x²＋y²＝5、x²＋y²＝（√5）²」となり、半径√5の円となる。

先生　さて、次は円の中心が原点O（0,0）以外の場合について取り上げてみよう。
生徒　かなり複雑になっていますね。
先生　そうか。それじゃあ、円の中心が原点O（0,0）のときの式と比べてみよう。何か気がつかない？
生徒　う～ん、そうだなぁ……。
先生　じゃあ、ヒントね。「平行移動」です。
生徒　あっ、xの代わりに（x－a）、yの代わりに（y－b）が使われています！
先生　うん、そうだね。中心は原点O（0,0）からx軸方向にaだけ、y軸方向にbだけ平行移動するから（a,b）になるんだ。
生徒　平行移動の考え方って、いろんな関数や方程式で使えるんですね。
先生　そう、その感覚を持つことが大切なんだ。このあと取り組む三角関数でも平行移動の考え方を利用するから、いまのうちにマスターしておくといいよ。最後に、円の方程式と平方完成の練習問題に取り組んで終わりにしよう。
生徒　はい、ありがとうございました！

練習問題
　次の式は円の方程式である。円の中心座標と半径を求め、グラフを描きなさい。
（1）（x－2）²＋（y－3）²＝4²
（2）（x＋1）²＋（y－1）²＝2
（3）x²－2x＋y²－8＝0
（4）x²＋y²＋4x＋2y＋4＝0

答
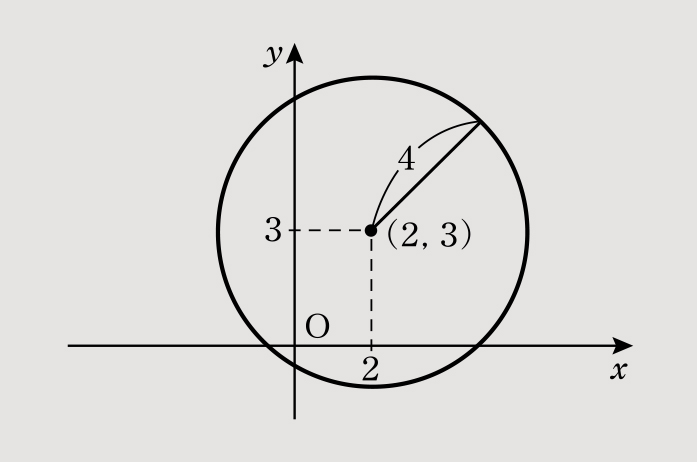
（1）中心（2,3）、半径4の円。グラフは以下となる。

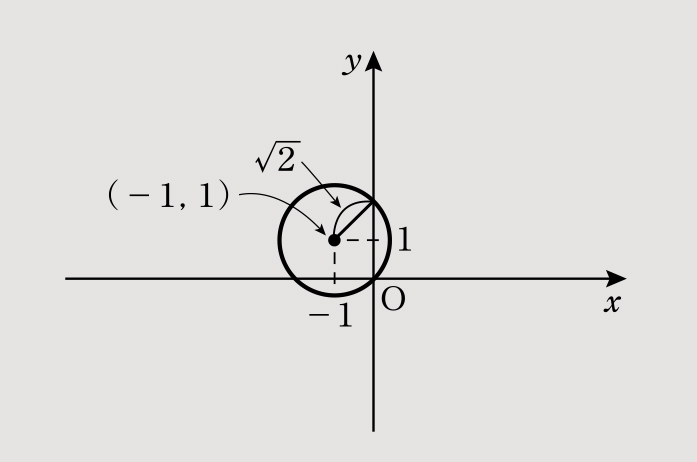
（2）「（x＋1）²＋（y－1）²＝2、（x＋1）²＋（y－1）²＝（√2）²」となり、中心（－1,1）、半径√2の円となる。

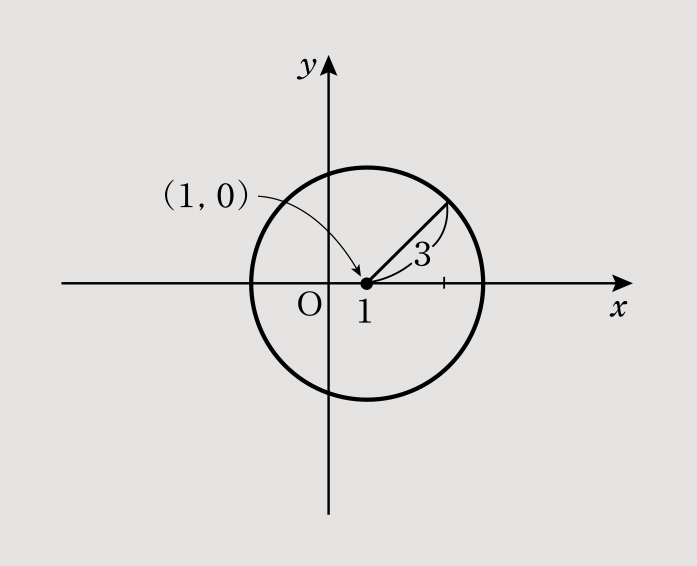
（3）x²－2x＋y²－8＝0をxについて平方完成すると「x²－2x＋y²－8＝0、（x－1）²－1＋y²－8＝0、（x－1）²＋y²＝9＝3²」となり、中心（1,0）、半径3の円となる。

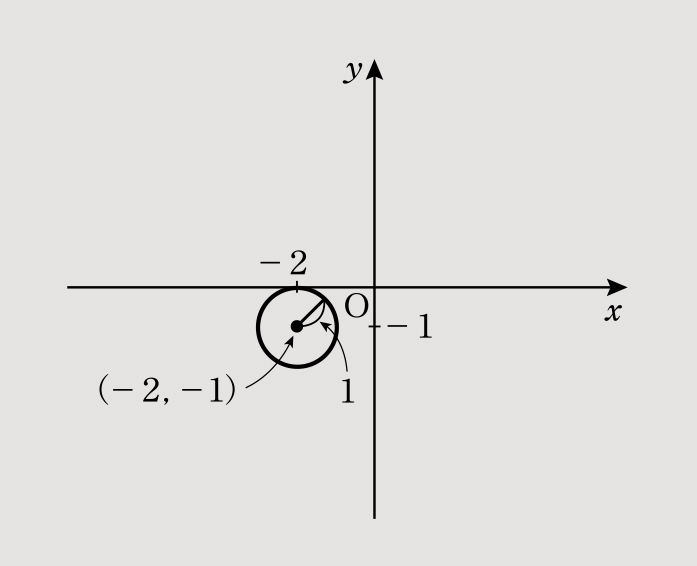
（4）x²＋y²＋4x＋2y＋4＝0をxについて平方完成すると「（x＋2）²－4＋y²＋2y＋4＝0」となり、同様にyについて平方完成すると「（x＋2）²－4＋y²＋2y＋4＝0、（x＋2）²－4＋（y＋1）²－1＋4＝0、（x＋2）²＋（y＋1）²＝1²」となり、中心（－2,－1）、半径1の円となる。