License
二次関数を習得する【電気数学のすゝめ20】
電験取得のための第一歩
2025.10.06
20限目
二次関数
先生 前回は一次関数y=ax+bと連立方程式の関係を取り上げたね。
生徒 はい。グラフの交点が連立方程式の解になるんですよね。
先生 うん、しっかりマスターしているね。それでは、次のテーマに入ろう。今回は二次関数だ。
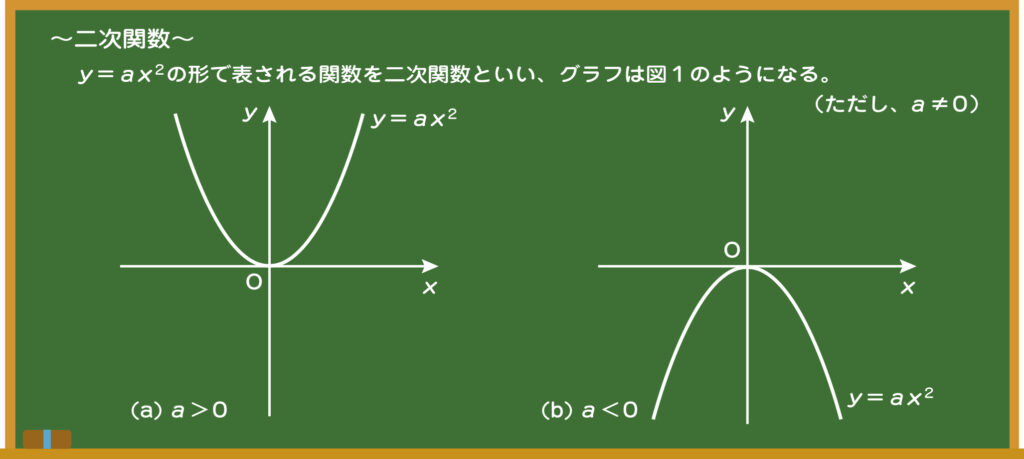
先生 まずは基本的な二次関数から始めるけど、黒板の図をみて何か気がつくことはあるかな?
生徒 う~ん、グラフが曲線になっている……!?
先生 そうだね。二次以上の関数は曲線のグラフになるんだ。この二次関数は「放物線」といって、物体を放り投げたときに描く軌跡が放物線になるから、そのまま「放物線」と呼ぶんだよ。ほかには?
生徒 a>0とa<0で上下が逆になっています。
先生 うん、正解。a>0のグラフを「下に凸」、a<0のグラフを「上に凸」と表現するんだ。よく使うから、覚えておこう。
生徒 はい。
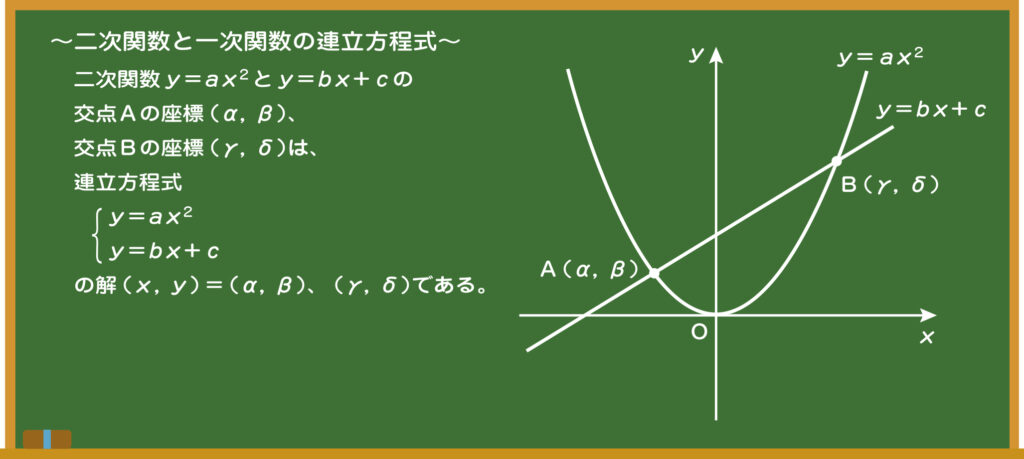
先生 黒板にあるように、二次関数もグラフ同士の交点と連立方程式の解は関係があるんだ。
生徒 交点の座標が方程式の解になるんですよね。
先生 そうなんだけど、二次関数で重要なのは、二次方程式だから解は2つあるということだ。つまり、交点も2つになるんだよ。
生徒 グラフにすると、解が2つあることが一目瞭然ですね。
先生 グラフのメリットは「解のみえる化」ができることなんだ。よし、ここで練習問題に取り組んでみよう。
練習問題
次の関数のグラフを描き、交点を求めなさい。
(1)y=x2とy=-5x-6
(2)y=x2とy=4x-3
(3)y=-x2とy=4x+4
(4)y=x2とy=2x-3
答
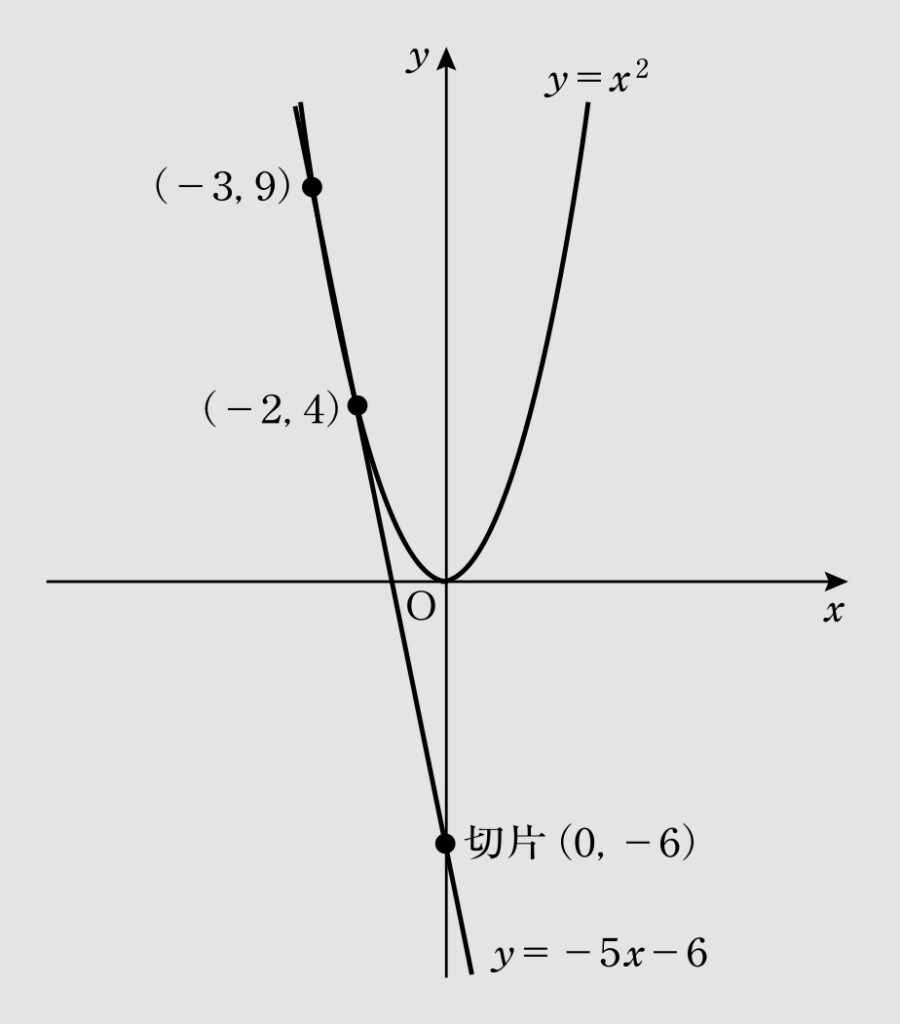
(1)グラフは図1に示す。交点は以下の連立方程式より求める。
y=x2 ……①
y=-5x-6……②
①-②より「0=x2+5x+6」となり、この二次方程式を解くと「x2+5x+6=(x+3)(x+2)=0」から「x=-2、-3」と求めることができる。
ここから「x=-2のときy=(-2)2=4、x=-3のときy=(-3)2=9」となり、したがって、それぞれ交点は(-2,4)(-3,9)となる。
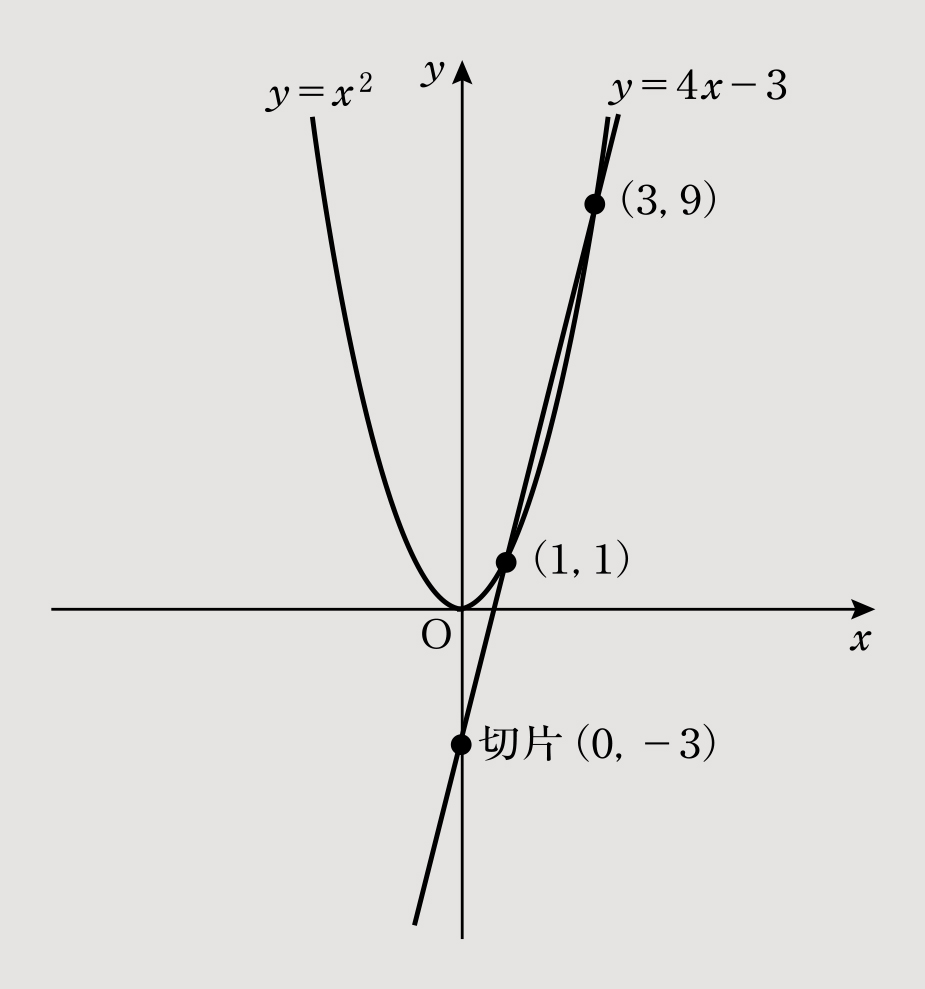
(2)グラフは図2に示す。交点は以下の連立方程式より求める。
y=x2 ……③
y=4x-3……④
③-④より「0=x2-4x+3」となり、この二次方程式を解くと「x2-4x+3=(x-3)(x-1)=0」から「x=3、1」と求めることができる。
ここから「x=3のときy=32=9、x=1のときy=12=1」となり、したがって、それぞれ交点は(3,9)(1,1)となる。
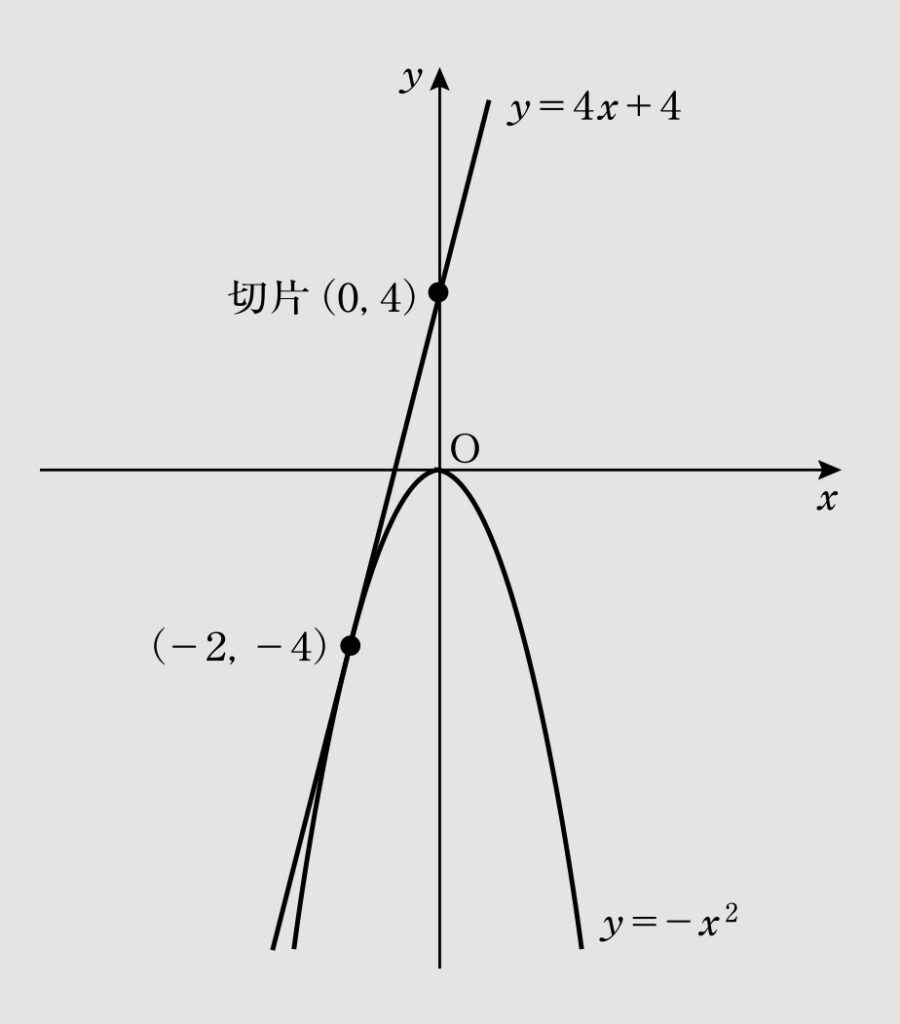
(3)グラフは図3に示す。交点は以下の連立方程式より求める。
y=-x2 ……⑤
y=4x+4……⑥
⑤-⑥より「0=-x2-4x-4=x2+4x+4」となり、この二次方程式を解くと「x2+4x+4=(x+2)2=0」から「x=-2」と求めることができる。
ここから「x=-2のときy=-(-2)2=-4」となり、したがって、交点は(-2,-4)となる。
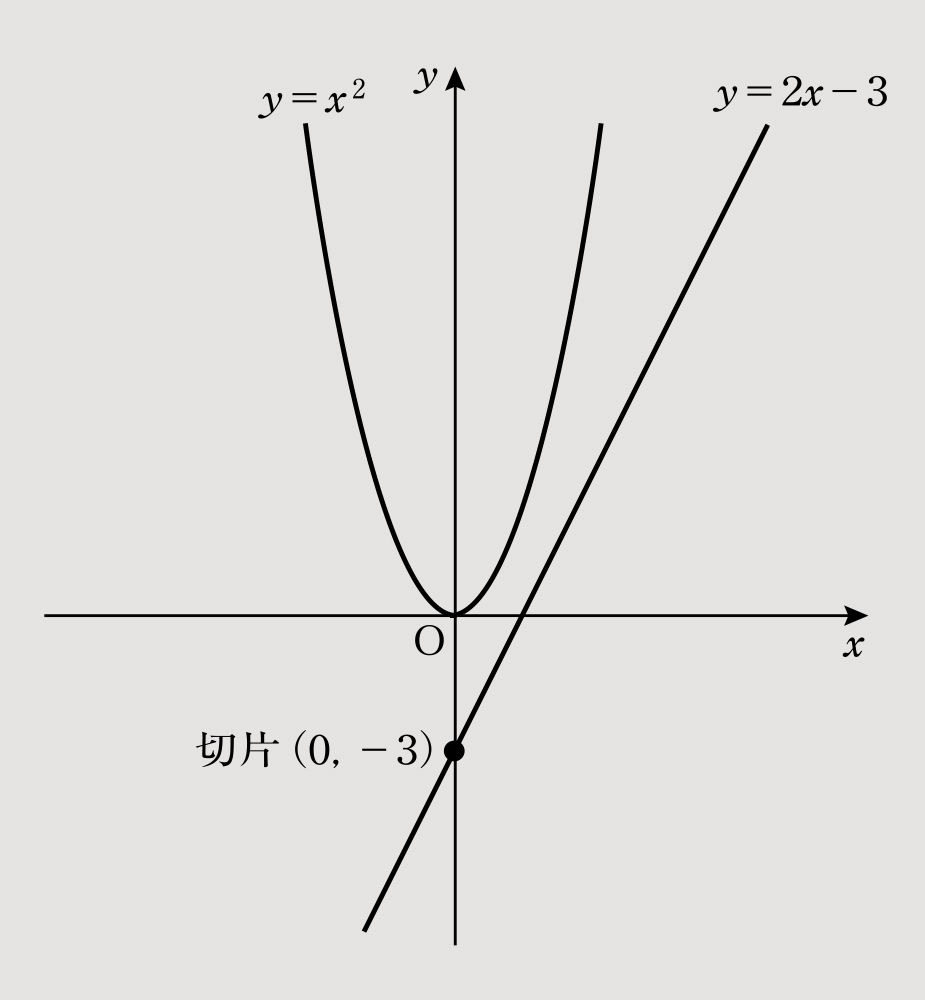
(4)グラフは図4に示す。交点は以下の連立方程式より求める。
y=x2 ……⑦
y=2x-3……⑧
⑦-⑧より「0=x2-2x+3」となり、この二次方程式を解の公式(x=
)を用いて解くと「x=1±√-2=1±j√2」と求めることができる。
図4のグラフからもわかるように、解が虚数を含む複素数のときは実数の交点は存在しない。したがって、交点はない。
先生 しっかり解けたかな?
生徒 問題(4)は悩みましたけど、ほかの3問はバッチリです! グラフにすると二次方程式が2つの解を持つことがわかりますね。
先生 うん、そういうことだ。問題(4)は解に虚数が含まれる場合で、解説していなかったけど、実数解がないからグラフは交点を持たないんだよ。
生徒 それを先に言ってほしかったです。
先生 まあまあ、グラフが描ければ交点がないことはわかるから、それができていればOKだよ。
生徒 は~い。
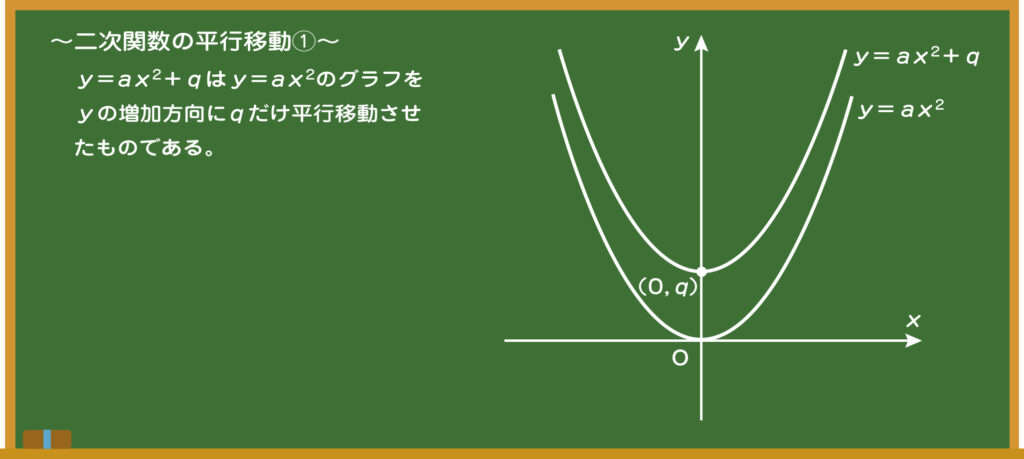
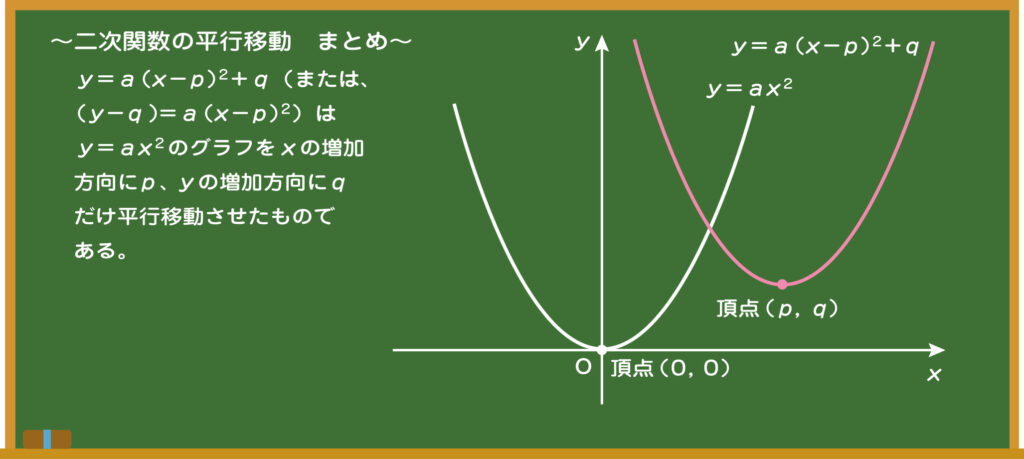
先生 一次関数と同様に、二次関数も平行移動を考えることができるんだ。まずはy軸方向の平行移動で、これは単純に「+q」をするだけ。qの符号がプラスならy=ax2はqだけ上に平行移動して、マイナスなら下に平行移動するというものなんだ。
生徒 一次関数のときと同じですね。
先生 うん、そういうこと。簡単でしょう? 次はx軸方向への平行移動を考えてみよう。
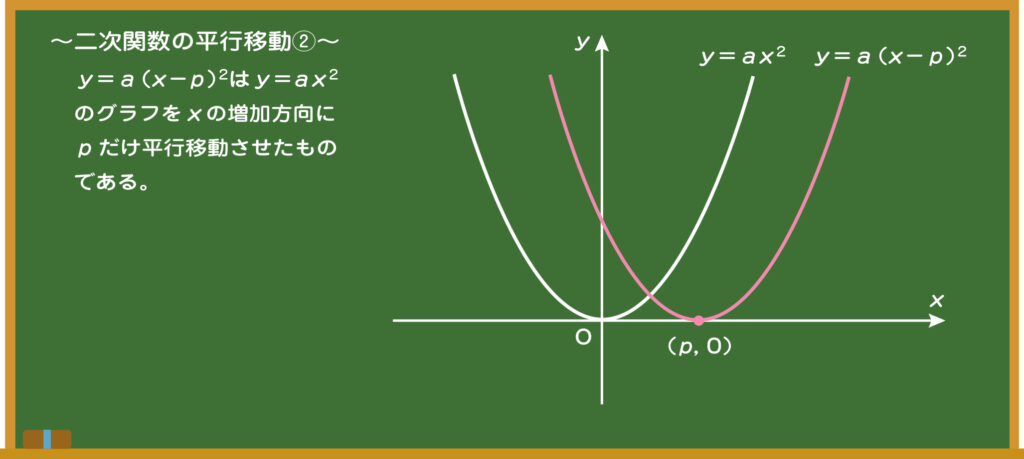
先生 y軸方向の平行移動とは少し違うでしょう。
生徒 はい、少し複雑になったような……。
先生 一般に、平行移動は「xを(x-p)に置き換える」と考えるんだ。例えば、y=2x2をx軸方向に1だけ平行移動した場合の式は「xを(x-1)に置き換える」からy=2(x-1)2となるんだよ。
生徒 あれ? この考え方はy軸方向の平行移動にはあてはまらない……。x軸とy軸では方法が違うんですね。
先生 そう思うでしょう。じゃあ、y=ax2+qを(y-q)=ax2と変換するとわかりやすいかな。「yを(y-q)に置き換える」とy=ax2をy軸方向にqだけ平行移動しているでしょう?
生徒 そうか、qを左辺に移項するのか!
先生 うん、そういうこと。これでx軸方向にもy軸方向にも平行移動できることがわかったよね。ちなみに「y=a(x-p)2+q」の座標(p, q)が頂点になるんだ。さて、練習問題で確認してみようか。
生徒 はい。
練習問題
次の関数の式を求めてグラフを描きなさい。また、頂点の座標を求めなさい。
(1)y=2x2をx軸方向に3、y軸方向に-4だけ平行移動した関数
(2)y=-3x2をx軸方向に-1、y軸方向に2だけ平行移動した関数
答
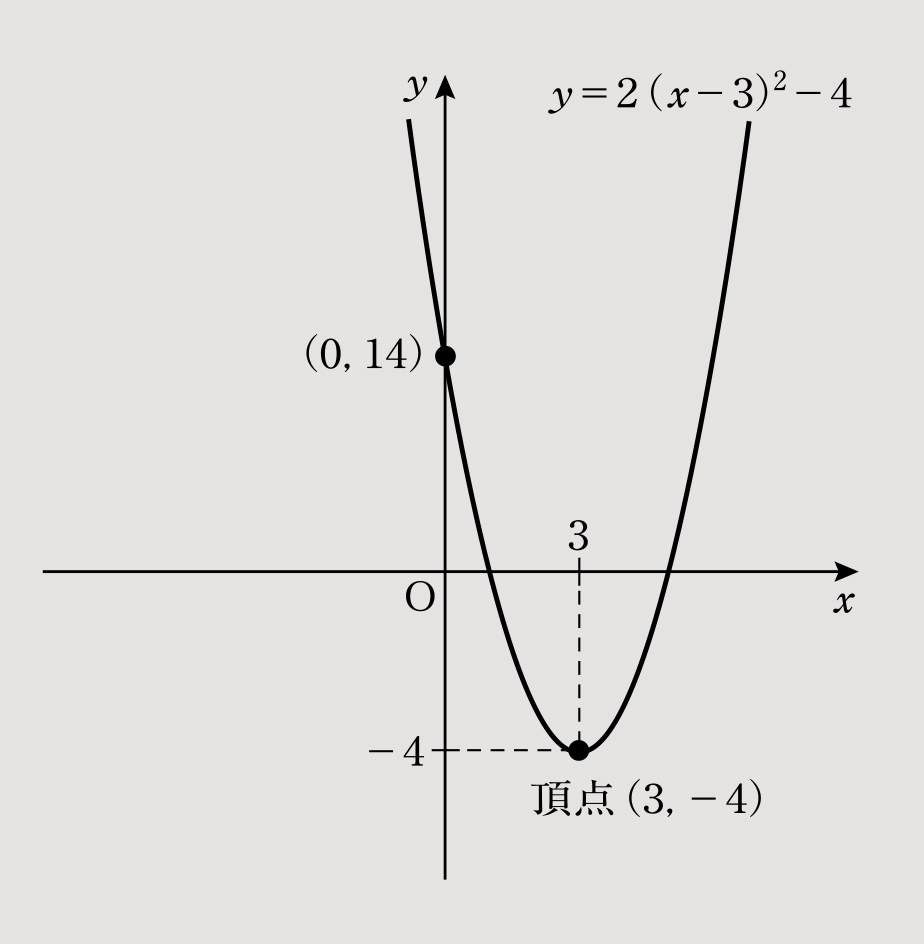
(1)関数の式はy=2(x-3)2-4となり、グラフは図1、頂点の座標は(3,-4)となる。
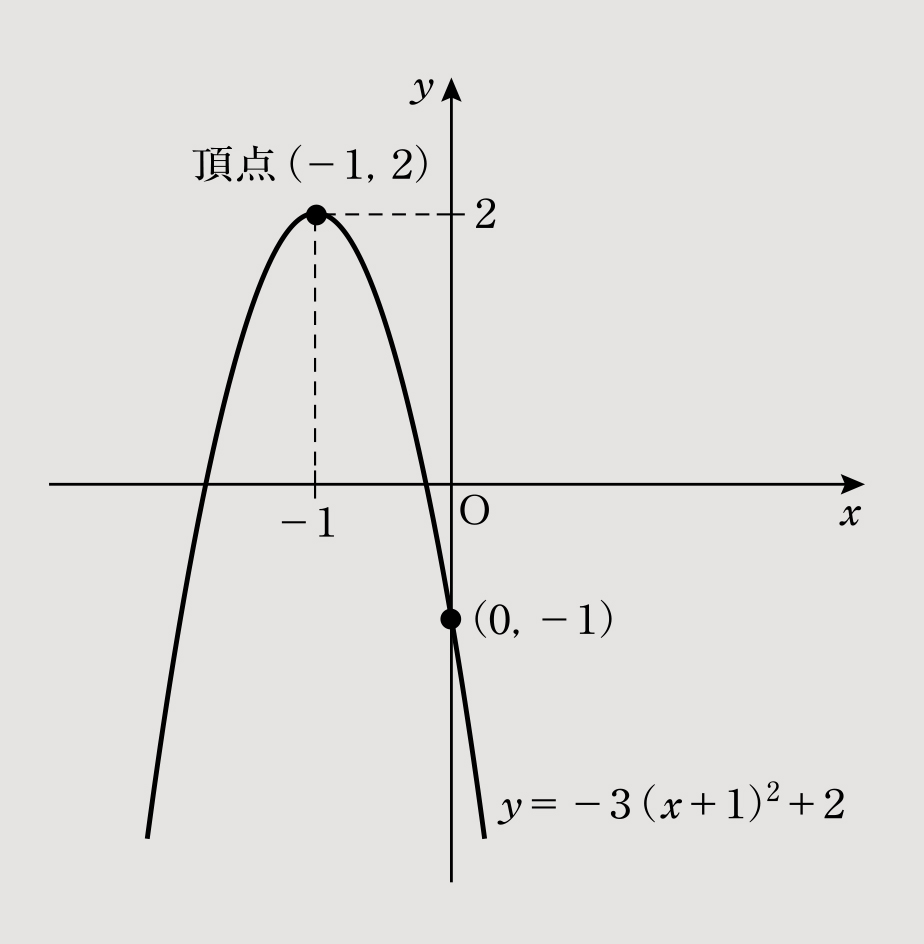
(2)関数の式はy=-3{x-(-1)}2+2=-3(x+1)2+2となり、グラフは図2、頂点の座標は(-1,2)となる。

先生 ところで、平方完成は覚えている?
生徒 二次方程式でやった「ムリやり(x+a)2をつくる技」ですよね?
先生 うん。例えば「2x2+4x+6」を平方完成すると、どうなるかな?
生徒 「2x2+4x+6=2(x2+2x)+6=2(x+1)2-2+6=2(x+1)2+4」となります。
先生 うん、OKだ。二次関数2x2+4x+6を平方完成してy=2(x+1)2+4になった。このように変換すると何ができるかな?
生徒 二次関数のグラフが描けます!
先生 うん、正解。それでは練習問題に取り組んで今回は終わりにしよう。
生徒 はい、ありがとうございました!
練習問題
次の関数のグラフを描き、頂点の座標を求めなさい。
(1)y=x2+6x+10
(2)y=-2x2-4x-5
答
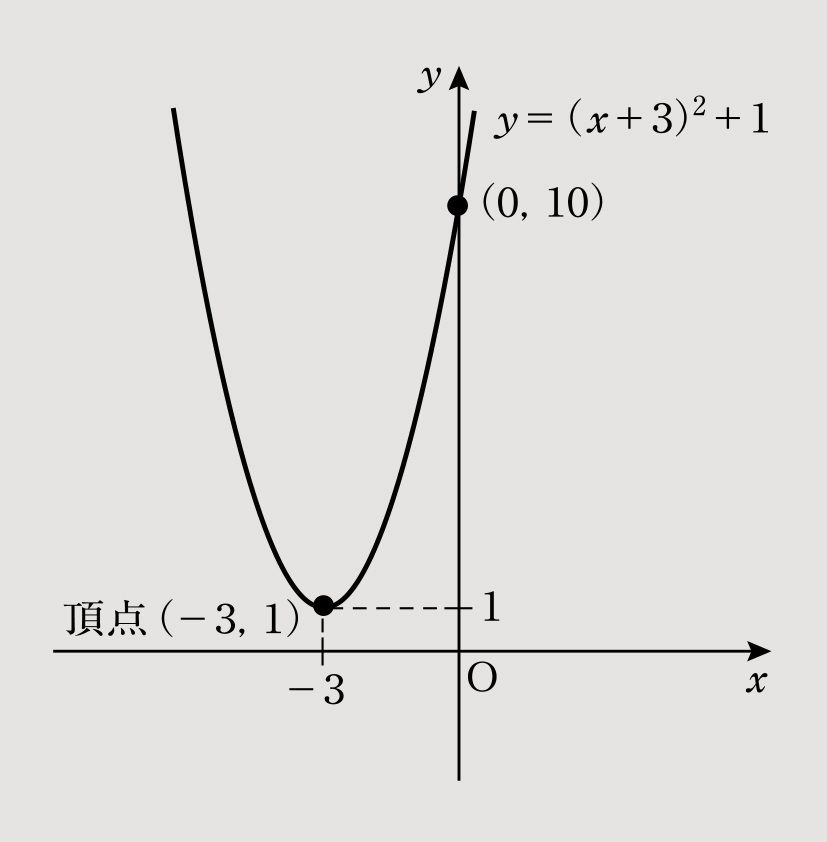
(1)y=x2+6x+10を平方完成すると「y=x2+6x+10=(x+3)2-9+10=(x+3)2+1」となる。
したがって、グラフは図1、頂点の座標は(-3,1)となる。
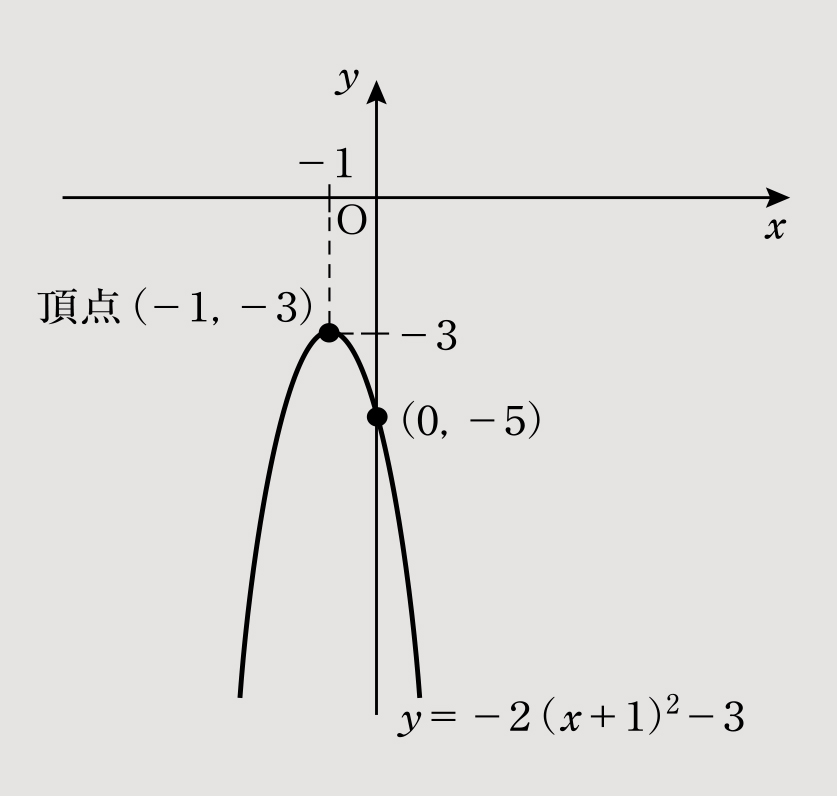
(2)y=-2x2-4x-5を平方完成すると「y=-2x2-4x-5=-2(x2+2x)-5=-2(x+1)2+2-5=-2(x+1)2-3」となる。
したがって、グラフは図2、頂点の座標は(-1,-3)となる。
講師/村山 慎一
関連記事

License

License

License

License

How to

How to
License

How to