二次方程式の解法を習得する【電気数学のすゝめ17】

電験取得のための第一歩

2025.04.28

17限目　二次方程式

先生　前回は一次方程式と連立方程式について学習したね。しっかり復習したかな？
生徒　はい、カンペキです！
先生　それじゃあ、次の問題はわかるかな？
　2x＋4y＝14
　 x＋2y＝7
生徒　まず、xを消去したいから下の式に「2」をかけてxの係数をそろえます。
　2x＋4y＝14……①
　2x＋4y＝14……②
　あれ、同じ式になっちゃった……。どうすればいいんだ？
先生　このように、連立方程式が同じ式になる場合、解は無限個あるから、この方程式は解けないんだよ。
生徒　え～っ、それはズルイ！　でも、なんで無限個あるってわかるんですか？
先生　解を整数に絞って考えてみようか。条件は「x＋2y＝7を満たすxとy」だから、例えば、（x，y）＝（1，3）（－1，4）（3，2）とかがあてはまるかな。分数とか実数、複素数を含めれば、いくらでも解はあるよね。
生徒　だから解は無限個なんだ。
先生　このような場合を不定というんだ。解が1つに定まらないからね。
生徒　ふ～ん。
先生　あまりピンときていないようだけど……。それじゃあ、次の問題をやってみてよ。
生徒　これも同じようにイジワルな問題なんじゃないですか？
先生　どうだろうね～。まあ、やってみてよ。
　2x＋4y＝14
　4x＋8y＝10
生徒　まずはxを消去するために上の式に「2」をかけてxの係数をそろえます。
　4x＋8y＝28……①
　4x＋8y＝10……②
　①式－②式を計算すると……　あれ、yも消えちゃった。
先生　うん、これも解けない方程式だよ。
生徒　やっぱり！
先生　でも、さっきの問題と違うところは、この方程式は解がないということなんだ。
生徒　解がない？
先生　うん。2つの方程式を同時に満たすx、yがないということだよ。
生徒　なんで「解がない」ってわかるんですか？
先生　①式－②式を計算すると「0＝18」となって、式として成り立たないよね。こんなときは解けないんだ。方程式をグラフに描いたり、「行列」という数学を使っても説明できるよ。そして、このような場合を不能というんだ。解くことができないからね。
生徒　解けないなら、やっても意味がないんじゃないですか？
先生　そんなことないよ。方程式をたてるとき、解が不能だったら、どこかに誤りがあることがわかるよね。不定になった場合は同じ条件で式をたてているから、別の条件を使って式をたてる必要があるんだよ。
生徒　不定や不能になったら、しっかり見直しをするってことですね。
先生　そういうことだ。通常、問題は解けるようになっているはずだからさ。さて、ここで質問。連立方程式をたてるとき、いくつの式が必要になるかわかるかな？
生徒　x、yのときは2つで、x、y、zのときは3つだったから、文字の数だけ必要だと思います。
先生　そう、正解だ。わからない値（x、y、zなどの未知数）の数だけ式をたてる必要があるんだよ。電気回路の問題で連立方程式を使うけど、求めたい未知数をできるだけ簡単に求められるように、連立方程式をたてることがポイントになるんだ。
生徒　は～い。

先生　それでは、ここから今回のテーマである「二次方程式」について学習しよう。二次方程式の一般式は「ax²＋bx＋c＝0（ただし、a≠0）」で表しているよ。
生徒　うわっ、難しそう……。
先生　大丈夫。簡単な二次方程式なら、すでに取り組んでいるんだよ。「平方根」は覚えているよね。4の平方根は？
生徒　±2です！
先生　うん、正解。実は、これも二次方程式なんだよ。x²＝4という二次方程式を解いたことになるんだ。式で表すと「x＝±2」だ。
生徒　一般式は難しそうだけど、ずいぶん簡単に感じますね。
先生　一般式に「a＝1」「b＝0」「c＝－4」を代入すると「x²－4＝0、x²＝4」になるでしょう。だから、二次方程式なんだよ。
生徒　なるほど！
先生　まずは練習問題で確認してみよう。

練習問題
　次の二次方程式を解け。
（1）x²＝9 （2）x²＝25 （3）x²＝3 （4）x²＝10

答
（1）x＝±3
（2）x＝±5
（3）x＝±√3
（4）x＝±√10

先生　できたかな？
生徒　はい！　余裕ですよ。
先生　うん、それでは次の段階にいこう。「x²＋5x＋6＝0」は解けるかな？
生徒　うわっ、いきなり難易度が上がった！
先生　この問題も前に取り組んだことがある知識で解けるよ。
生徒　う～ん、ヒントください！
先生　それじゃあ、左辺を因数分解してみてよ。
生徒　因数分解……!?　そうなると「x²＋5x＋6＝（x＋2）（x＋3）」です。
先生　うん、正解だ。もう、ほとんど解けたも同然だよ。
生徒　えっ、どうすればいいの？
先生　因数分解して「（x＋2）（x＋3）＝0」という式に変形できたよね。右辺は「0」だ。かけ算で0になるということは、どちらかの数が0ということ。つまり「（x＋2）＝0」か「（x＋3）＝0」となる。これを解くと？
生徒　「x＋2＝0」の場合は「x＝－2」で、「x＋3＝0」の場合は「x＝－3」です。因数分解して、かけ算の形に変換すれば解けるんだ！
先生　うん、そういうこと。よし、すぐに練習問題で確認しよう。

練習問題
　次の二次方程式を解け。
（1）x²＋3x＋2＝0 （2）x²＋4x＋4＝0
（3）x²＝4 （4）2x²＋20x＋48＝0

答
（1）x²＋3x＋2＝0、（x＋1）（x＋2）＝0、x＋1＝0またはx＋2＝0、x＝－1、－2
（2）x²＋4x＋4＝0、（x＋2）²＝0、x＋2＝0、x＝－2
（3）x²＝4、x²－4＝0、（x＋2）（x－2）＝0、x＋2＝0またはx－2＝0、x＝－2、2
（4）2x²＋20x＋48＝0、2（x²＋10x＋24）＝0、x²＋10x＋24＝0（両辺を2でわる）、（x＋4）（x＋6）＝0、x＋4＝0またはx＋6＝0、x＝－4、－6

先生　どう、できたかな？
生徒　（2）は少し不安でした。x＝－2だけでいいのかなって。
先生　うん、鋭いね。実は、二次方程式の解は必ず2つあるんだ。
生徒　でも、（2）は1つだけですよね。
先生　この場合、x＝－2またはx＝－2というように解が2つあると考えるんだ。この状態を重解といって、まさしく、解が重なっているという意味ね。それでも値が同じだから表記は1つしかないんだよ。
生徒　そうなんですね。
先生　ちなみに、三次方程式には解が3つ、四次方程式には解が4つ、n次方程式には解がn個ある。これを「代数の基本定理」というんだ。
生徒　（3）は式を変形すると、解がプラスとマイナスの2つあることがわかります。この式をみたら、これまでは「±○」って答えるんだって暗記していました。
先生　これで「平方根は？」という問題に、プラスとマイナスの2つの解がある意味がわかったでしょう。
生徒　はい！

先生　さて、次にいこうか。「x²＋10x＋2＝0」は、どう考えるかな？
生徒　因数分解もできないし、どうすればいいんだ……。
先生　この問題は「平方完成」というテクニックが必要になるんだ。
生徒　平方完成って？
先生　（x＋a）²を強引につくる方法なんだ。この問題では「x²＋10x」の部分に着目してみよう。x²＋10xから（x＋a）²をつくるには、どうすればいいかな？
生徒　う～ん。
先生　ヒントね。x²＋10x＋25だったら？
生徒　x²＋10x＋25＝（x＋5）²です……　あっ、（x＋a）²の形ができた！
先生　でも、実際はx²＋10xだ。さて、どうする？
生徒　両辺から25をひきます。「x²＋10x＋25－25＝（x＋5）²－25、x²＋10x＝（x＋5）²－25」になります。
先生　正解！　これが平方完成だ。そこで、問題の方程式をみてみよう。「x²＋10x＋2」だから、どうする？
生徒　「x²＋10x＋2＝（x＋5）²－25＋2＝（x＋5）²－23＝0、（x＋5）²＝23」です。
先生　よし、もうひと息だ。x²＝aの二次方程式の解はx＝±√aだよね。ここで（x＋5）²＝23の（x＋5）をAと置いたら、x²＝aの形にならないかな？
生徒　（x＋5）²＝23で（x＋5）＝Aと置くとA ²＝23、つまり、A＝±√23ということですか？
先生　うん。ただし、求めるのはxだから、Aをxが入った形に変換しよう。
生徒　x＋5＝Aだから「A＝±√23、x＋5＝±√23、x＝－5±√23」です！
先生　正解、よくできました！
生徒　一応はできたけど、平方完成のコツは、まだつかめていません……。
先生　それじゃあ、平方完成の例を挙げてみようか。アンダーラインの値に注目すると、ある規則に気づくと思うよ。「①x²＋10x＝（x＋5）²－5²、②x²＋6x＝（x＋3）²－3²、③x²＋8x＝（x＋4）²－4²、④x²＋5x＝（x＋ $\frac{5}{2}$ ）²－（ $\frac{5}{2}$ ）²、⑤x²＋x＝（x＋ $\frac{1}{2}$ ）²－（ $\frac{1}{2}$ ）²」だけど、どうかな？
生徒　あっ、xの係数を2でわった値で平方完成しています！
先生　うん。じゃあ、x²＋axを（x＋○）²の形にすると、どうなる？
生徒　（x＋ $\frac{a}{2}$ ）²です。
先生　OK！　それじゃあ、x²＋axと（x＋ $\frac{a}{2}$ ）²を等しくするには、どうすればいい？
生徒　（x＋ $\frac{a}{2}$ ）²＝x²＋ax＋（ $\frac{a}{2}$ ）²だから、両辺から（ $\frac{a}{2}$ ）²をひけば等しくなります！
先生　そう、正解だ。練習問題で確認しておこう。

練習問題
　次の二次方程式を解け。
（1）x²＋3x＋1＝0 （2）x²＋6x－4＝0
（3）x²＋8x＋4＝0 （4）2x²＋8x－3＝0

答
（1）x²＋3x＋1＝0
（x＋ $\frac{3}{2}$ ）²－（ $\frac{3}{2}$ ）²＋1＝0、（x＋ $\frac{3}{2}$ ）²＝（ $\frac{3}{2}$ ）²－1＝ $\frac{9}{4}$ －1＝ $\frac{5}{4}$
（x＋ $\frac{3}{2}$ ）＝± $\sqrt{\frac{5}{4}}$ 、x＝± $\sqrt{\frac{5}{4}}$ － $\frac{3}{2}$ ＝ $\frac{- 3 \pm \sqrt{5}}{2}$
（2）x²＋6x－4＝0
（x＋3）²－3²－4＝0、（x＋3）²＝9＋4＝13、（x＋3）＝±√13
　x＝±√13－3＝－3±√13
（3）x²＋8x＋4＝0
（x＋4）²－4²＋4＝0、（x＋4）²＝4²－4＝16－4＝12
（x＋4）＝±√12、x＝±√12－4＝－4±2√3
（4）2x²＋8x－3＝0
　2（x²＋4x－ $\frac{3}{2}$ ）＝0、x²＋4x－ $\frac{3}{2}$ ＝0、（x＋2）²－2²－ $\frac{3}{2}$ ＝0、（x＋2）²＝ $\frac{3}{2}$ ＋4＝ $\frac{11}{2}$
（x＋2）＝± $\sqrt{\frac{11}{2}}$ 、x＝± $\sqrt{\frac{11}{2}}$ －2＝± $\frac{\sqrt{11} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}$ －2＝ $\frac{- 4 \pm \sqrt{22}}{2}$

先生　さあ、できたかな？
生徒　（4）は少し悩みました。
先生　この問題は「x²の係数でくくる」がポイントだね。それじゃあ、仕上げに「解の公式」に取り組もう。
生徒　まだあるのか……。
先生　これが最後だから、集中していこう！
生徒　は～い。

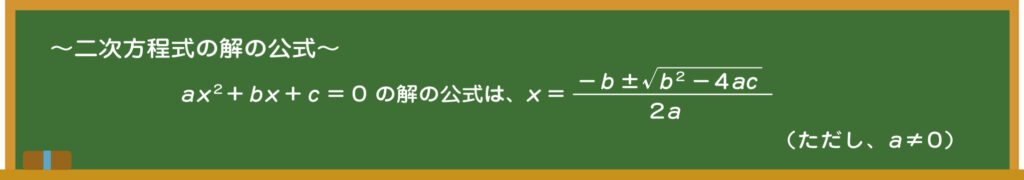
先生　実は、この公式があれば、すべての二次方程式は解けるんだ。だから、しっかり暗記しておこう。
生徒　何だか大変そう。
先生　何度も書いていけば、イヤでも覚えるよ。さあ、ラストスパートだ！　練習問題に取り組んで終わりにしよう。
生徒　は～い、ありがとうございました～。

練習問題
　次の二次方程式を解け。
（1）2x²＋4x－1＝0 （2）x²＋2x＋8＝0

答
（1）二次方程式の係数はa＝2、b＝4、c＝－1だから、これを解の公式に代入して求める。
　x＝ $\frac{- b \pm \sqrt{b^{2} - 4 ac}}{2 a} = \frac{- 4 \pm \sqrt{4^{2} - 4 \times 2 \times (- 1)}}{2 \times 2} = \frac{- 4 \pm \sqrt{16 + 8}}{4} = \frac{- 4 \pm \sqrt{24}}{4}$
　＝ $\frac{- 4 \pm 2 \sqrt{6}}{4} = \frac{- 2 \pm \sqrt{6}}{2}$
（2）二次方程式の係数はa＝1、b＝2、c＝8だから、これを解の公式に代入して求める。
　x＝ $\frac{- b \pm \sqrt{b^{2} - 4 ac}}{2 a} = \frac{- 2 \pm \sqrt{2^{2} - 4 \times 1 \times 8}}{2 \times 1} = \frac{- 2 \pm \sqrt{4 - 32}}{2} = \frac{- 2 \pm \sqrt{- 28}}{2}$
　＝ $\frac{- 2 \pm j \sqrt{28}}{2} = \frac{- 2 \pm j 2 \sqrt{7}}{2}$ 　＝－1±j√7