一次関数を習得する【電気数学のすゝめ18】

電験取得のための第一歩

2025.07.07

18限目　一次関数（1）

先生　前回のテーマは二次方程式だ。いろいろな解法に取り組んだけど、覚えているかな？
生徒　はい。でも、解の公式が不安ではあります。
先生　少し複雑だからね。二次方程式の解の公式に限らず、数学の公式は丸暗記しようとすると大変だから、公式を導き出せるようになることが重要なんだ。
生徒　すごい複雑なんですけど、導けるんですか？
先生　もちろん。でも、問題のたびに公式を導くことは大変だよね。だから、自然と覚えてしまうくらい、何度も何度も問題に取り組むことが大切なんだ。
生徒　は～い。

先生　さて、そろそろ授業に入ろうか。今回は「関数」について学習しよう。まずは最も基本的な一次関数からだ。
生徒　一次関数ということは、二次関数も三次関数もあるということですか？
先生　うん。xの最大次数が一次ならば一次関数、二次ならば二次関数。例えば「y＝5x」は一次関数、「y＝2x²＋5x＋1」は二次関数になるんだ。電験三種では複雑な関数は出題されないけど、グラフの読み方と深く関係しているから、しっかり学んでいこう。
生徒　はい！
先生　それじゃあ、関数の基本から取り組むよ。金貨1枚は銀貨5枚と交換できるとすると、下の表はどうなると思う？

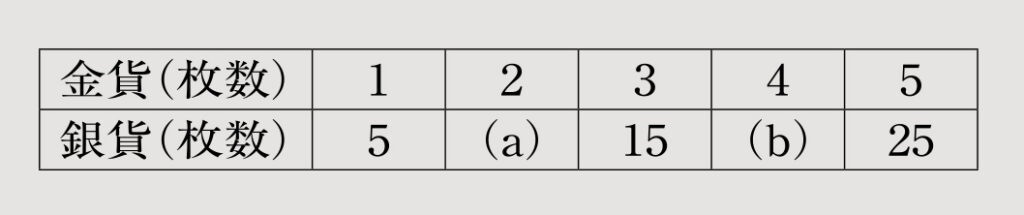
生徒　（a）には10、（b）には20が入ります。
先生　うん、正解だ。どうやって求めた？
生徒　（a）は5×2＝10で、（b）は5×4＝20です。
先生　それじゃあ、金貨x枚を、すべて銀貨に交換すると、銀貨の枚数はどうなるかな？
生徒　銀貨は金貨の5倍の枚数に交換できるから「5x枚」です。
先生　そうだね。ここで、銀貨の枚数をyとすると「y＝5x」という関係式ができるよね。このようにyをxの式で表せるとき「yはxの関数である」というんだ。そして、xの次数は一次だから、これを一次関数と表現するんだよ。
生徒　う～ん……。
先生　少しややこしいかな。じゃあ、関数のイメージを両替機で考えてみようか。今回の例だと、金貨を入れて銀貨が出てくる両替機。xを入れて（入力して）、yが出てくる（出力される）装置と考えると、この装置が関数ということになるんだよ。
生徒　少しわかってきました。
先生　もっと簡単に言うと、y＝axのaを求めることができれば、関数を求めたことになるんだ。この場合はy＝5xだから、a＝5だね。
生徒　aを求めればいいってことなんですね。
先生　y＝axの場合はね。このaを「比例定数」、または「傾き」と呼んでいるんだ。いまは関数の初歩だから求める値はaのみだけど、少しずつ増えていくから、しっかり基礎を固めておこう。まずは、練習問題で確認だ。
生徒　は～い。

練習問題
　次の表の（a）（b）（c）を求めよ。なお、xとyはy＝2xの関係にあるものとする。

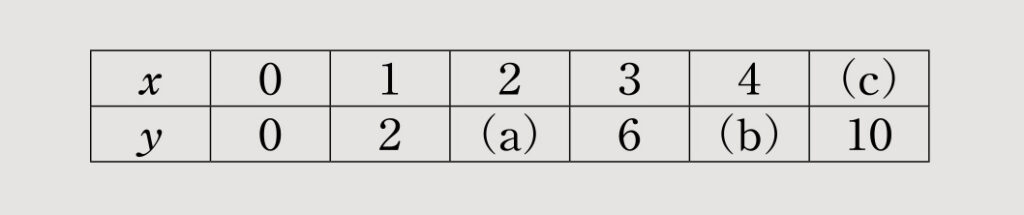
答
（a）y＝2xにx＝2を代入すると、y＝2×2＝4
（b）y＝2xにx＝4を代入すると、y＝2×4＝8
（c）y＝2xにy＝10を代入すると、10＝2x、x＝5

練習問題
　次の表は関数y＝axのxとyの値である。比例定数aを求めよ。

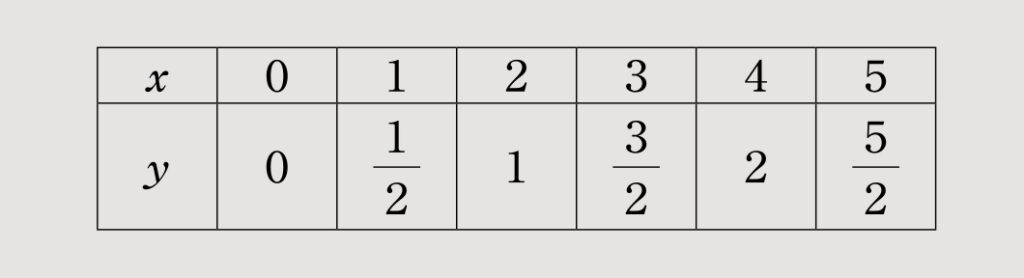
答
　y＝axに（x, y）＝（1, $\frac{1}{2}$ ）を代入すると「 $\frac{1}{2}$ ＝a×1、a＝ $\frac{1}{2}$ 」となる。
　したがって、求める関数はy＝ $\frac{1}{2}$ xとなる。
　なお、ほかの表の値（x, y）＝（2,1）（3, $\frac{3}{2}$ ）（4,2）（5, $\frac{5}{2}$ ）を代入してもa＝ $\frac{1}{2}$ を求めることができる。

先生　できたかな？
生徒　はい、余裕です！
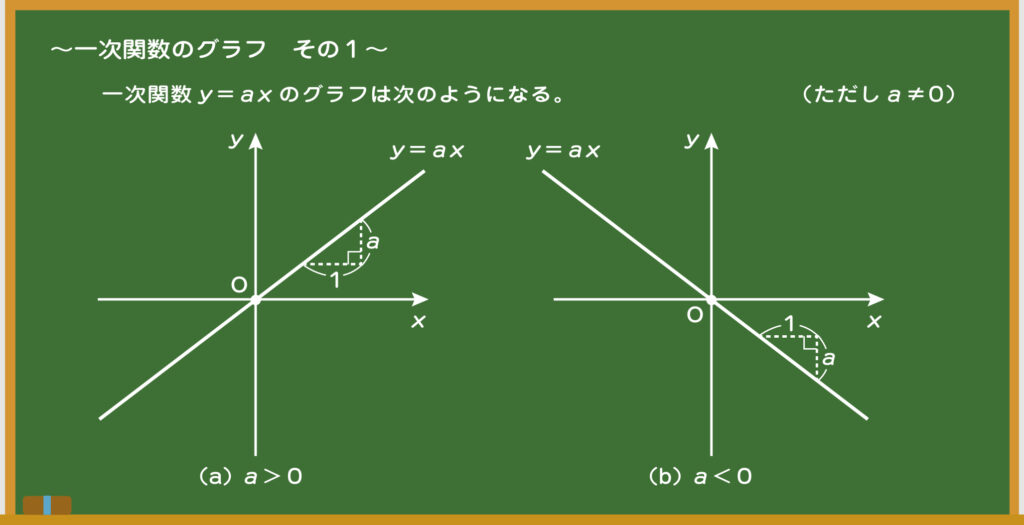
先生　うん、それじゃあ、次は「グラフの描き方」だ。ポイントは3つで「①y＝axは原点O（0,0）を通る」「a＞0ならば右上がり、a＜0ならば右下がり」「③y＝axは直線である」が成り立っているんだよ。
生徒　う～ん、言葉だけだと少しわかりづらいかな。
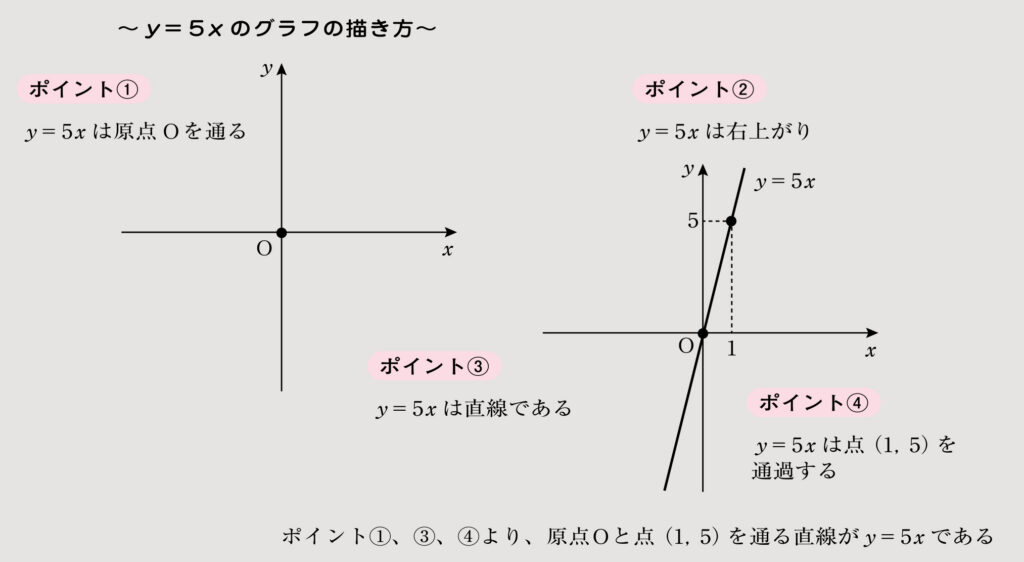
先生　まずは、試しにy＝5xのグラフを描いてみよう。ポイント①から、y＝5xは原点O（0,0）を通るから、原点O（0,0）に点を打っておこう。
生徒　はい。
先生　次に、ポイント②から、y＝5xだからa＝5になるよね。したがって、a＞0だからグラフは右上がりになって、ポイント③からy＝5xだからグラフは直線になることがわかる。
生徒　直線だとわかることに、何かメリットがあるんでしょうか？
先生　直線は通貨する点が2つわかれば、その2点を結んでグラフを描けるよね。
生徒　はい。
先生　y＝axの場合、1つは原点O（0,0）であることがわかっているから、あと1つだけ通過する点がわかればグラフは描けるよね？
生徒　そうか！　でも、原点以外の点って、どうやって求めればいいんですか？
先生　y＝5xに適当な値を代入すれば求められるよ。例えば、x＝1を代入したときのyの値は？
生徒　y＝5xにx＝1を代入すると、y＝5×1＝5です。
先生　うん。それじゃあ、その点の座標は？
生徒　（x, y）＝（1,5）です。
先生　正解。原点以外の点は別に（1,5）だけではないからね。y＝5xを満たす点なら、どこでもいいんだ。
生徒　（2,10）でもいいってことですよね？
先生　うん。わかってきたみたいだね。それじゃあ、グラフの描き方をまとめておくから、その間に練習問題に取り組んでみようか。

練習問題
　次の一次関数のグラフを描きなさい。
（1）y＝3x　（2）y＝－6x

答
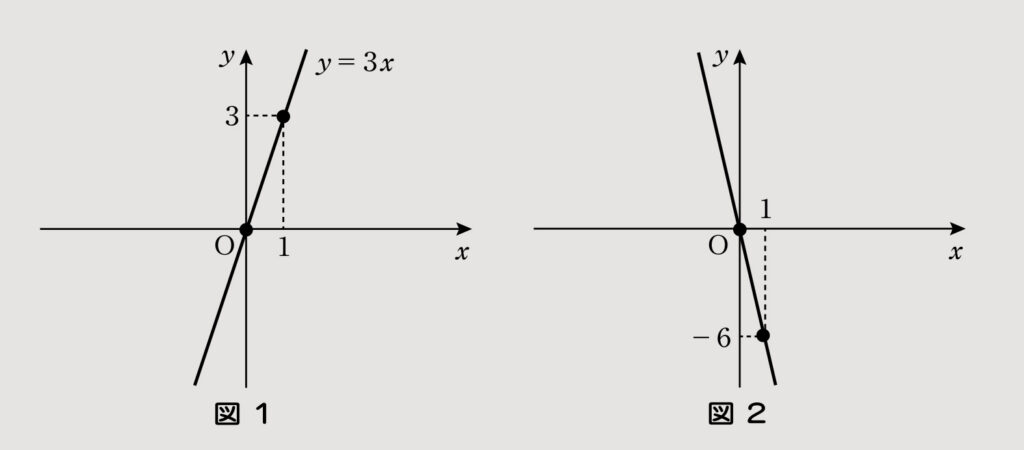
（1）グラフを描く手順を以下に示す。
①y＝3xは原点O（0,0）を通る。
②x＝1をy＝3xに代入すると、y＝3×1＝3となる。したがって、y＝3xは点（1,3）を通る。
③y＝3xは直線なので、原点O（0,0）と点（1,3）を通る直線を描く（図1）。
（2）グラフを描く手順を以下に示す。
①y＝－6xは原点O（0,0）を通る。
②x＝1をy＝－6xに代入すると、y＝－6×1＝－6となる。したがって、y＝－6xは点（1,－6）を通る。
③y＝－6xは直線なので、原点O（0,0）と点（1,－6）を通る直線を描く（図2）。

先生　今度はグラフから関数の式を導いてみようか。
生徒　y＝axのaを求めればいいんですね。
先生　うん。y＝axのグラフの場合、原点O（0,0）以外に通る点がわかれば求められるよ。早速、練習問題に取り組んでみよう。

練習問題
　次のグラフを関数の式で表せ。ただし、関数はy＝axの形をしているものとする。

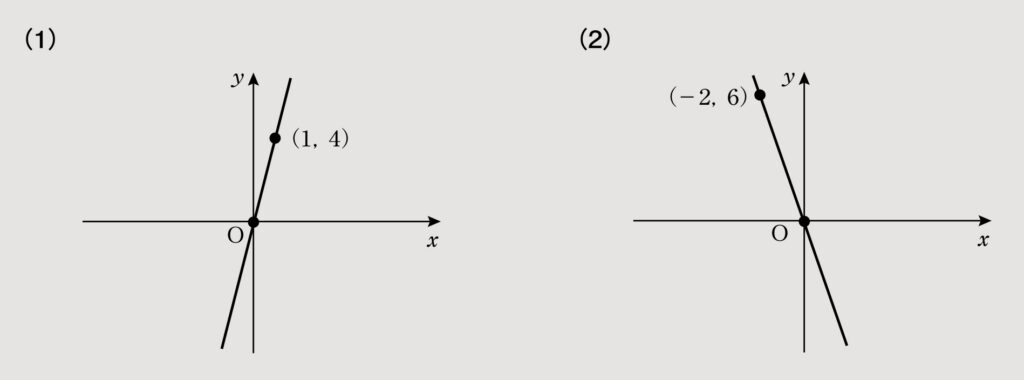
答
（1）点（1,4）を通るので、y＝axに（x,y）＝（1,4）を代入すると「4＝a×1、a＝4」となり、したがって、関数式はy＝4xと求めることができる。
（2）点（－2,6）を通るので、y＝axに（x,y）＝（－2,6）を代入すると「6＝a×（－2）、a＝ $\frac{6}{- 2}$ ＝－3」となり、したがって、関数式はy＝－3xと求めることができる。
先生　できたかな？
生徒　はい、バッチリです！
先生　今回の一次関数は原点O（0,0）を通るものだけを扱ったけど、それ以外の一次関数は次回に取り上げるから、楽しみにしていてね。
生徒　難しくなりそうですね……。
先生　基本的な解法は同じだから、関数の式を方程式にする方法さえ理解していればOK、大丈夫だよ。それじゃあ、今日は終わりにしよう。
生徒　はい、ありがとうございました。