How to
地絡電圧の考え方【「実務×理論」シリーズ4】
地絡現象~地絡電圧と地絡電流、電源電圧の関係に迫る~
2024.06.14
対地電圧と地絡電圧
非接地式配電線路では、配電線に分布する対地静電容量と、そこに流れる充電電流により各相の対地電圧が決まってくる。
各相の対地静電容量が等しい(平衡)状態の健全時では、大地の電位は電源電圧の中性点と同電位であるので、各相の対地電圧はバランスのとれた状態で運転される。
しかし、地絡が発生すると、地絡電流により地絡の発生した相の対地電圧は下降し、ほかの健全相の対地電圧は上昇してバランスが崩れてしまう。
今回は、このバランスの崩れた量(電位差)を「地絡電圧」と考え、地絡電圧、地絡電流、電源電圧の関係について取り上げる。
(1)非接地単相2線式配電線路
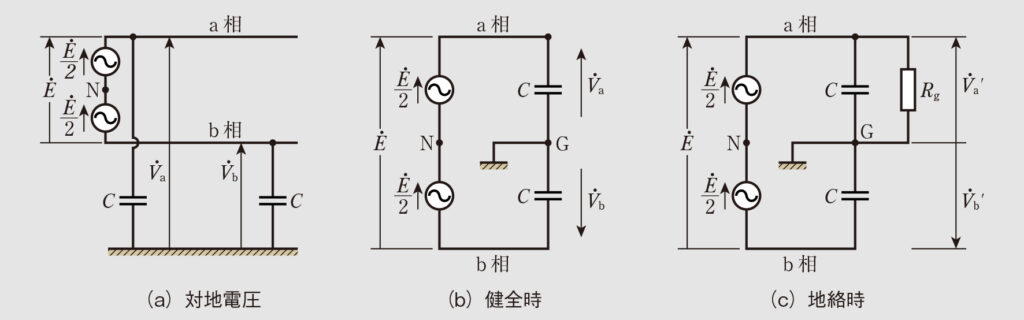
まずは、非接地式単相2線式配電線路の回路図を図1(a)、(b)に示す。電気的中性点Nを考えるために、電源電圧
を
ずつに分ける。各相の対地電圧を
、
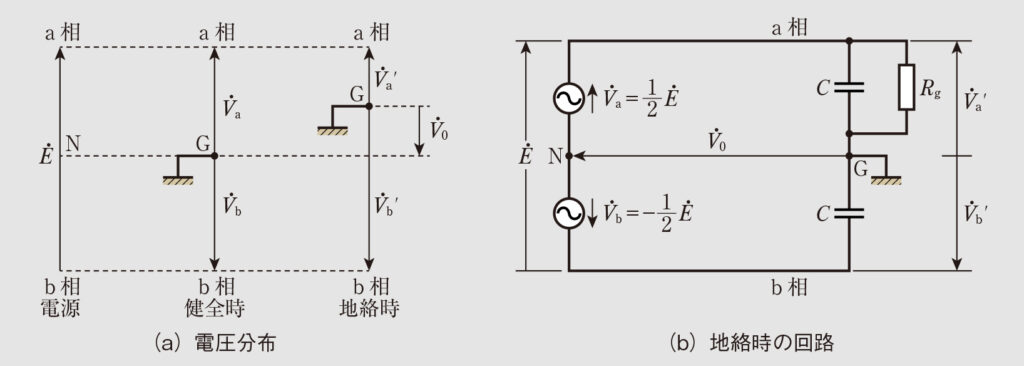
とおき、両電圧とも大地側をマイナス方向(矢尻)とする。また、各電圧のベクトルを位相差は考えず、直線上に表したものと図2(a)の「健全時」に示す。これより、
……(1)
となる。
したがって、健全時は大地の電位G点は電源電圧の中性点(電気的な中間点)Nと同電位にあり、この状態で安定して運転される。
a相で地絡が発生すると、図1(c)のようにa相の対地電圧は下降して
、b相の対地電圧は上昇して
となり、
となる。電源電圧
は不変であり、(1)式の関係は変わらないので、大地の電位点GはN点からa相側に移動する。
G点に対するN点の電位を
(大地側をマイナス方向)とすると、図2(a)の「地絡時」のようになり、回路図は図2(b)で表すことができる。この
を地絡電圧とすると、図2から、
(
は
と逆方向)……(2)
(
は
と同方向)……(3)
(2)および(3)式から、地絡が発生すると健全時の各相対地電圧に地絡電圧が加わり、その分、地絡相では電圧が下降し、そのほかの相では電圧が上昇することがわかる。
また、
であるから、この関係を(2)式+(3)式に代入すると、
……(4)
となる。
a相が完全地絡したときには
であるから、(4)式に代入して
となる。
また、前述のとおり(1)式は
と
の間にも成り立つから、
となる。
したがって、b相の対地電圧
は電源電圧
と同じ大きさになり、地絡電圧
は電源電圧
の大きさの
となる。
(2)非接地式三相3線式配電線路
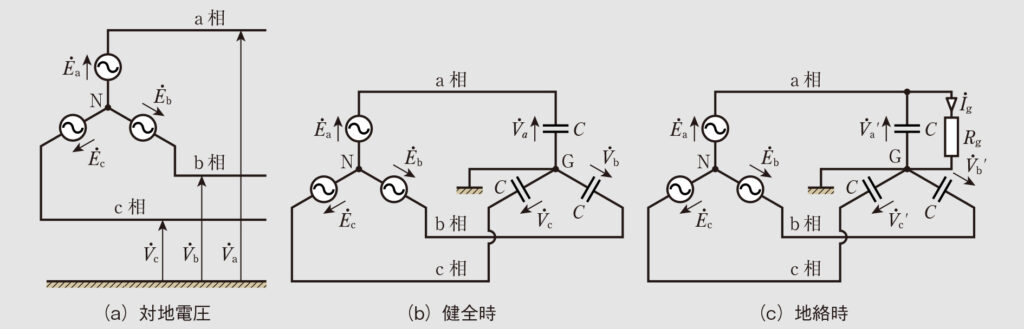
基本的には非接地式単相2線式配電線路の場合と同じである。図3(a)、(b)に非接地式三相3線式配電線路の回路図を示す。健全時において、電源は対称三相電圧、各相の相電圧を
、
、
、相回転はa→b→c、電気的中性点をN、大地の電位をG、各相の対地電圧を
、
、
とすると、N点とG点は同電位なので
となり、健全時はこの状態で安定して運転する。
図3(c)のようにa相で地絡が発生したとすると、a相の対地電圧
は下降し、b相の対地電圧
、c相の対地電圧
は上昇するので、G点はa相側に移動する。
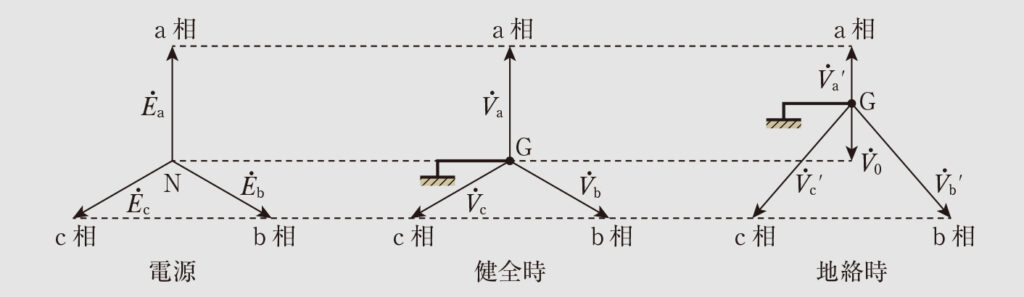
ここで、単相2線式配電線路の場合と同様に、各電圧の位相差を考えずに大地の電位G点は直線的に移動するものとしてベクトル図を描くと図4のようになるので、G点に対するN点の電位を地絡電圧
と考えることができる。
したがって、図4から、
……(5)
……(6)
……(7)
となる。
また、
であるから、この関係を(5)式+(6)式+(7)式に代入すると、
ここから、
……(8)
となる。
a相が完全地絡したときにはG点がa相まで移動するので、地絡電圧の大きさ
は相電圧に等しくなり、b、c相の対地電圧の大きさ
、
は線間電圧に等しくなる。
地絡電圧と地絡電流の関係
ZCTで検出した地絡電流値だけでは順方向か逆方向かを判別することはできない。地絡の方向は地絡電圧を検出し、その相互間の位相差から判別している。
したがって、地絡現象を理解するには地絡電圧と地絡電流の関係を知る必要がある。そこで、鳳-テブナンの定理を用いて地絡電流
を算出し、ここから地絡抵抗値
を∞~0で変化させたときの地絡電流と地絡電圧のベクトル軌跡を描いて関係を説明する。
(1)非接地単相2線式配電線路
図1(c)を、図5(a)のように地絡抵抗
を接続する端子を設け、
の接続点側からみた左側回路のインピーダンスを
、接続前の端子間の電圧を
とする。
次に、図5(b)のように接続後の
に流れる電流を地絡電流
として鳳-テブナンの定理より求めると、
、
……(9)
となるので、図5(b)の回路図は図5(c)のように
と
の直列回路として 書き換えられる。なお、図5では地絡抵抗
を可変抵抗と考え、健全時
から完全地絡時
の過程を表すものとする。
図5(c)のように
の端子電圧を
、
の端子電圧を
とすると、
となる。
ここで、回路のインピーダンスを
、アドミタンスを
、原点を0、横軸を実数、縦軸を虚数、
を基準ベクトルとして、各ベクトル図および軌跡を描くと図6のようになる。以下に
へ変化させたときの各ベクトルの軌跡の特徴を挙げる。
①
の軌跡は実軸に平行な直線となり、
から
へ向かう。
②
の軌跡は0点から反時計回りに半円の軌跡を描き、j2ωCへ向かう。半円の直径は2ωCとなる。
③
なので、
の大きさは
のEt倍、位相は
と同相、直径2ωCEtの半円となる。
④
は
なので、直径
の半円となり、位相は-jがつくので
より
遅れた軌跡となる。
⑤
は
なので、位相は
と同相になる。
図6の結果を図2(a)の「地絡時」のベクトル図にあてはめてみる。
(a)
図5(a)の
は地絡前(
未接続)のa相対地電圧
だから、
となる。
(b)
図1(c)の電圧
と図5(c)の
は、
に
が流れたときの電圧降下を示しているので
となる。
(c)
図2(b)より、図5(c)にN点および電圧
を描くと図5(c’)のようになる。これより
であることがわかる。
これらを図7に示す。これより、以下のことがわかる。
①大地の電位は地絡抵抗
=∞→0へ変化すると、0点から直径
の半円の軌跡を描きながらa相まで移動する。
②大地の電位が移動するにつれて、各相の対地電圧や地絡電圧も半円の軌跡となる。
③地絡電流
の軌跡は直径2ωCEの半円を描き、位相はa相の対地電圧と同相となり、
より
[rad]遅れる。
④(2)、(3)式は成り立つので(4)式が成り立ち、
である。
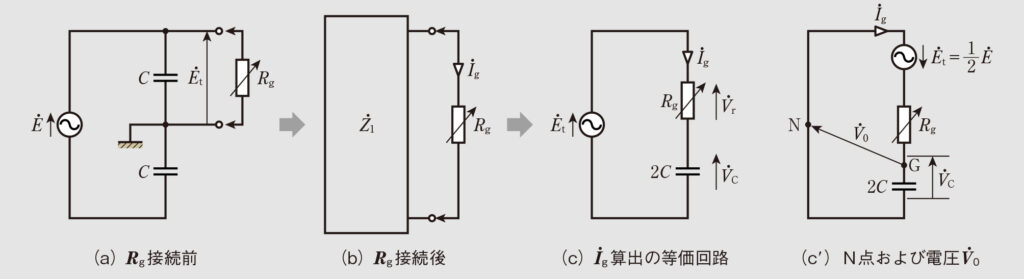
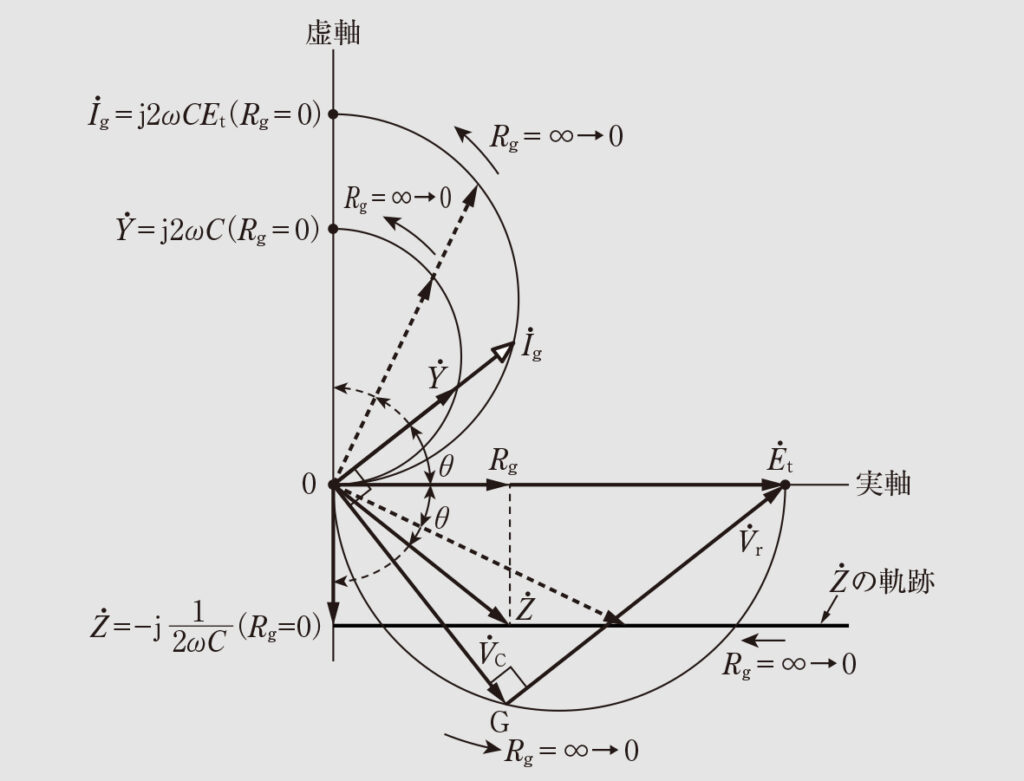
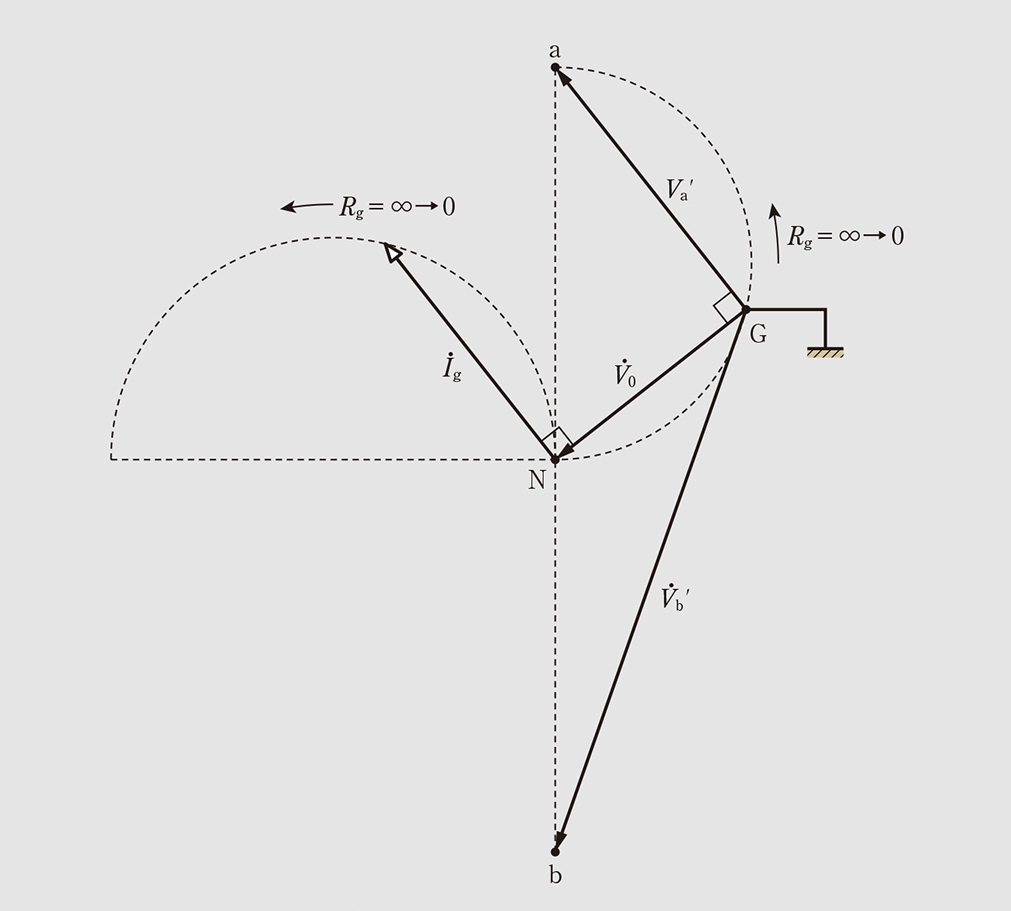 図7 単相2線式配電線路における
と
の軌跡
図7 単相2線式配電線路における
と
の軌跡(2)非接地式三相3線式配電線路
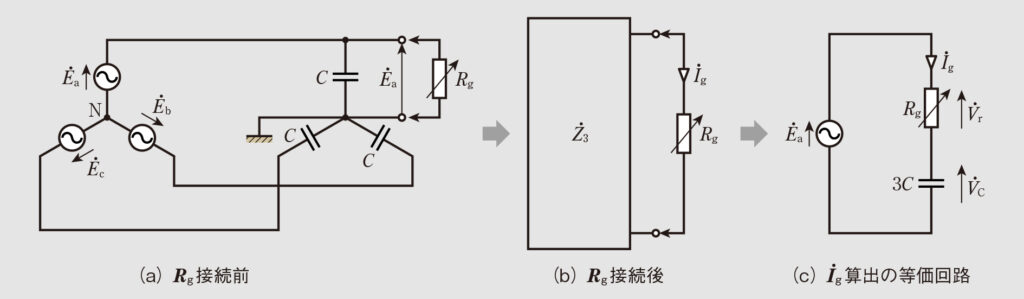
非接地単相2線式配電線路と同様に、図3(c)において図8(a)のように地絡抵抗
を接続する端子を設け、
の接続点側からみた回路のインピーダンスを
、接続前の端子間の電圧を
とする。
次に、図5(b)のように接続後の
に流れる電流を地絡電流
として、鳳-テブナンの定理より求めると、
……(10)
となり、図8(c)のように変換することができる。
ここで、図8(c)は図5(c)において、
を
(a相の相電圧)、2Cを3Cに置き換えただけなので、図8(c)の各ベクトル軌跡は図6と同じように考えられる。
したがって、この結果を図4のベクトルで
を
、
を
、
を
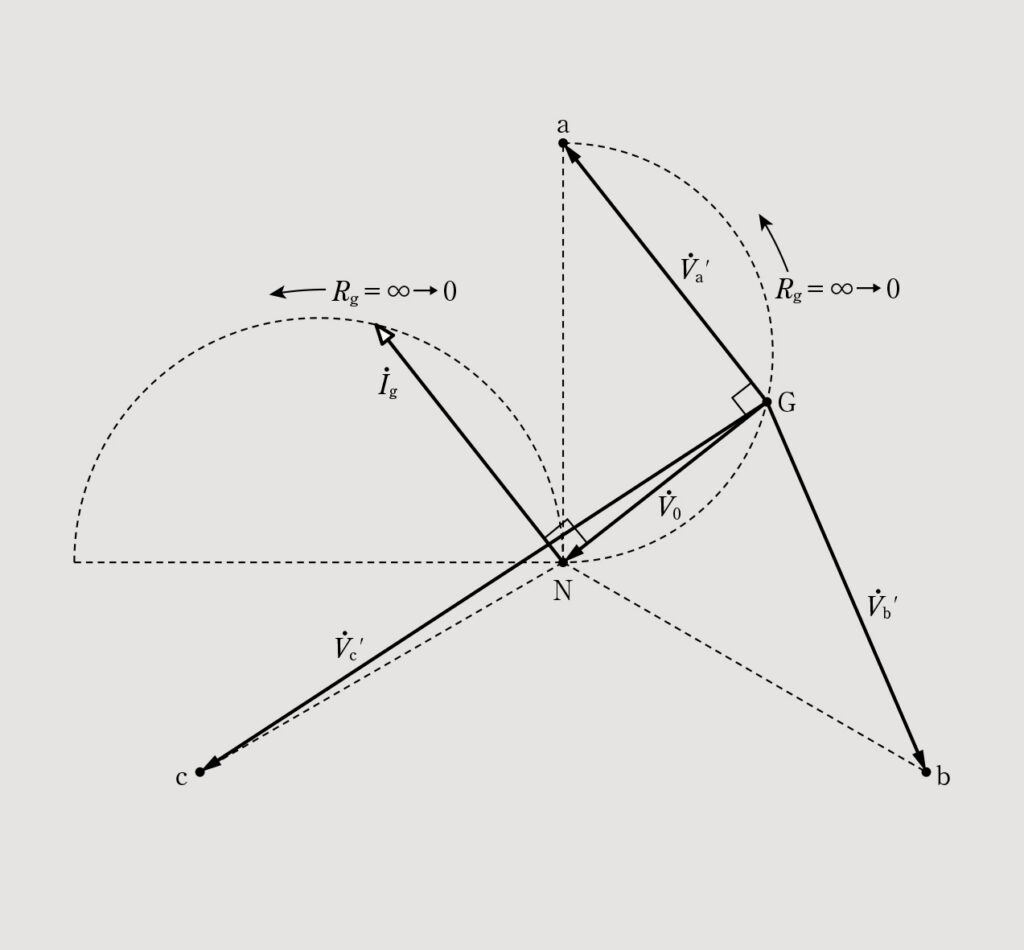
と、それぞれ置き換えてみると図9のようになる。ここから以下のことがわかる。
①大地の電位は地絡抵抗
=∞→0へ変化すると、0点から直径Eaの半円の軌跡を描きながらa相まで移動する。
②大地の電位が移動するにしたがって、各相の対地電圧や地絡電圧も半円の軌跡を描く。
③地絡電流
の軌跡は直径3ωCEの半円を描き、位相はa相の対地電圧と同相となり、
より
[rad]遅れる。
④(5)、(6)、(7)式は成り立つので(8)式は成り立ち、
である。
(3)地絡電流の方向判別
=∞→0において、地絡電流と地絡電圧には
[rad]の位相差があるので、検出した地絡電流が地絡電圧より
[rad]遅れるのか、進んでいるのかを判別すれば、地絡の発生した箇所がZCTを設置した箇所より、K側かL側かを知ることができる。これは地絡保護を行う場合に、地絡が保護範囲内で発生したものであるか否かを判別するときに用いられる。
文/古屋 正道
このシリーズ
「実務×理論」シリーズ関連記事

How to

How to

How to

How to

How to

License

License

How to