電気回路への応用を学習する【電気数学のすゝめ22】

電験取得のための第一歩

2026.02.18

22限目
電気回路への応用①

先生　前回は反比例と円のグラフで、最近は数学に近い内容を取り上げていたけど、今回のテーマは電気回路だ。
生徒　久しぶりだ！　7限目「合成抵抗の計算その4」で学習して以来です。
先生　あのときは合成抵抗の計算方法には触れたけど、抵抗の電気的なイメージは省略したよね。今回は抵抗、電流、電圧のイメージと、電気回路で使用する公式について学ぶことにしよう。
生徒　はい。
先生　まずは、合成抵抗の復習から取り組んでみよう。

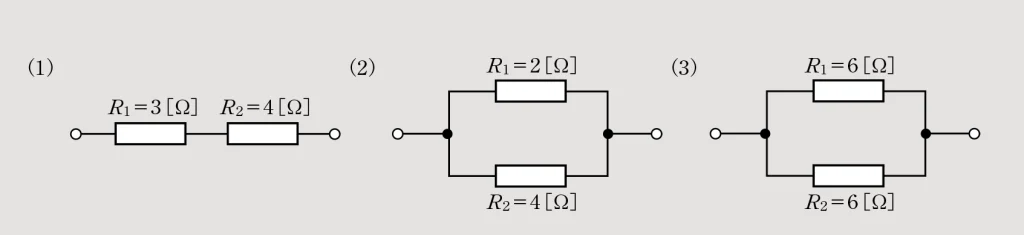
練習問題
　次の回路の合成抵抗R［Ω］を求めなさい。

答
（1）R＝R₁＋R₂＝3＋4＝7［Ω］
（2）R＝ $\frac{R_{1} \times R_{2}}{R_{1} + R_{2}}$ +＝ $\frac{2 \times 4}{2 + 4}$ ＝ $\frac{8}{6}$ ＝ $\frac{4}{3}$ ［Ω］
（3）R＝ $\frac{R_{1} \times R_{2}}{R_{1} + R_{2}}$ ＋＝ $\frac{6 \times 6}{6 + 6}$ ＝ $\frac{36}{12}$ ＝3［Ω］

先生　さて、できたかな？
生徒　はい、バッチリ！
先生　それでは、具体的に「抵抗」について考えてみよう。まず、電気回路には「電流」が流れるよね。電流は水の流れをイメージするとわかりやすいよ。
生徒　はい。
先生　そのとき、抵抗は電流の「流れにくさ」を表すことになる。水にたとえると、水の「流れにくさ」が抵抗になるんだ。
生徒　なるほど。
先生　ここで、図のような2本のホースを考えてみよう。どちらのホースが水が流れにくいと思う？

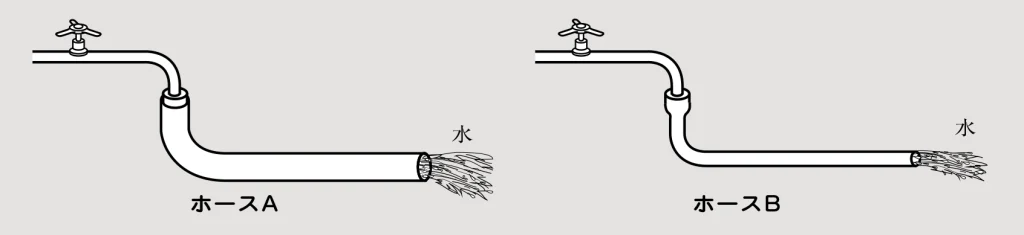
生徒　ホースBです。
先生　どうして？
生徒　細いからです。
先生　OK！　正解だ。それでは、次のケースでは？

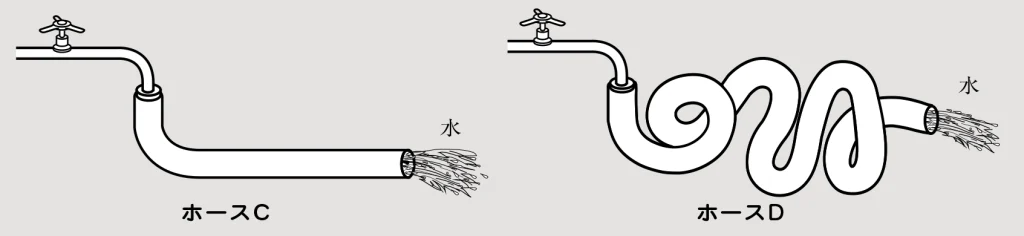
生徒　ホースDのほうが長いし、クネクネしているから流れにくいと思います。
先生　そう、正解。水の流れにくさとホースには「ホースが細いほど流れにくい」「ホースが長いほど流れにくい」という2つの関係があるんだ。これを電気に置き換えてみると、どうなると思う？　ちなみに、電気が流れるところは「導体」と表現しようか。
生徒　う～ん、導体が細いほど抵抗は大きくなるし、導体が長いほど抵抗は大きくなるってこと？
先生　うん、そうだね。これを数式化してまとめてみよう。

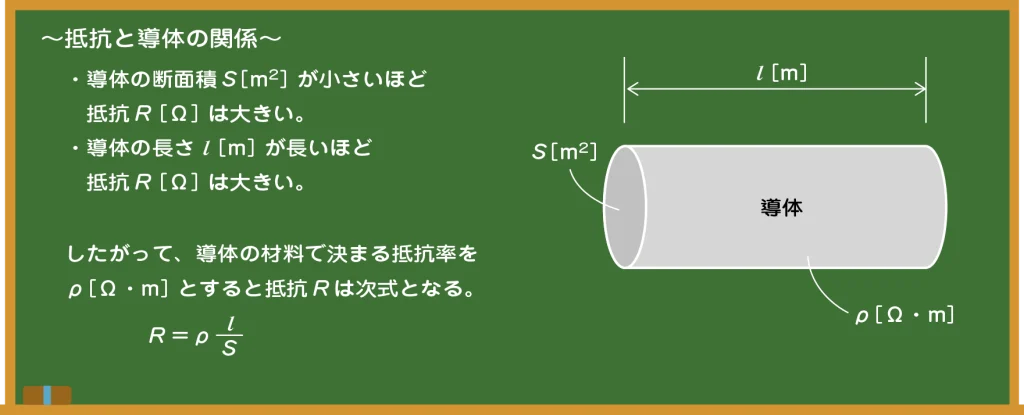
先生　黒板の式を比例、反比例という言葉を使って表現すると、どうなるかな？
生徒　抵抗Rは導体の長さlと抵抗率ρに比例し、導体の断面積Sに反比例します。
先生　OK！　ちなみに、抵抗は導体の温度が上がっても大きくなるんだ。
生徒　???
先生　温度が高いときは物質の原子の運動が激しくなって、電流の流れを妨げるからだよ。これも電気の学習が進めば扱う話だから、いまのうちから覚えておこう。
生徒　は～い。
先生　それじゃあ、練習問題に取り組んでみよう。

練習問題
（1）抵抗率ρ＝1.62×10^－8Ω・m、長さl＝2m、断面積S＝0.04m²の導体の抵抗R［Ω］を求めなさい。
（2）抵抗率ρ＝2.62×10^－8Ω・m、長さl＝100m、抵抗R＝0.05Ωの導体の断面積S［m²］を求めなさい。
（3）20℃において、ある銅線の電気抵抗を測定したところ、R₂₀＝6.45Ωであった。同様に40℃で同じ銅線の電気抵抗を測定したところ、R₄₀＝7.00Ωであった。銅線の抵抗温度係数α［1/K］を求めなさい。ただし、関係式はR₄₀＝R₂₀{1＋α（40－20）}＝R₂₀（1＋20α）［Ω］である。

答
（1）R＝ρ $\frac{l}{S}$ ＝ $\frac{1.62 \times 10^{- 8} \times 2}{0.04}$ ＝81.0×10^－8［Ω］
（2）S＝ρ $\frac{l}{S}$ ＝ $\frac{2.62 \times 10^{- 8} \times 100}{0.05}$ ＝52.4×10^－6［m²］
（3）関係式を「α＝」の形にするため、まず、両辺をR₂₀でわると「 $\frac{R_{40}}{R_{20}}$ ＝ $\frac{R_{20}}{R_{20}}$ （1＋20α）＝1＋20α」となる。
　これを変形すると「 $\frac{R_{40}}{R_{20}}$ －1＝20α、 $\frac{\frac{R_{40}}{R_{20}} - 1}{20}$ ＝ $\frac{20 α}{20}$ ＝α」となり、問題の数値を代入する。
　α＝ $\frac{\frac{R_{40}}{R_{20}} - 1}{20}$ ＝ $\frac{\frac{7.00}{6.45} - 1}{20}$ ≒0.004264＝ $\frac{1}{234.5}$ ［1/K］

先生　練習問題の解説をすると、（1）の導体の正体は銀なんだ。抵抗率が低い金属として有名で、オーディオにこだわる人は配線に銀を使ったりしているんだよ。
生徒　へぇ～。
先生　長さ2mで、抵抗は81.0×10^－8Ωと、ほぼゼロだね。だから、銅線の抵抗はゼロとみなすことができるんだ。
生徒　そうなんですね。
先生　（2）の導体はアルミニウムで、（3）は少し驚いたと思うけど、温度と抵抗の関係を扱った問題なんだ。
生徒　意味はわからなかったけど、数値を代入して何とか解けました。
先生　この問題も電験三種で出題されたことがあるんだ。ようするに、導体は温度が高くなると抵抗値が上がるということ。20℃で6.45Ωだけど、40℃では7.00Ωになっているでしょう。
生徒　あっ、ホントだ！
先生　さて、次は抵抗の接続方法について学習しよう。

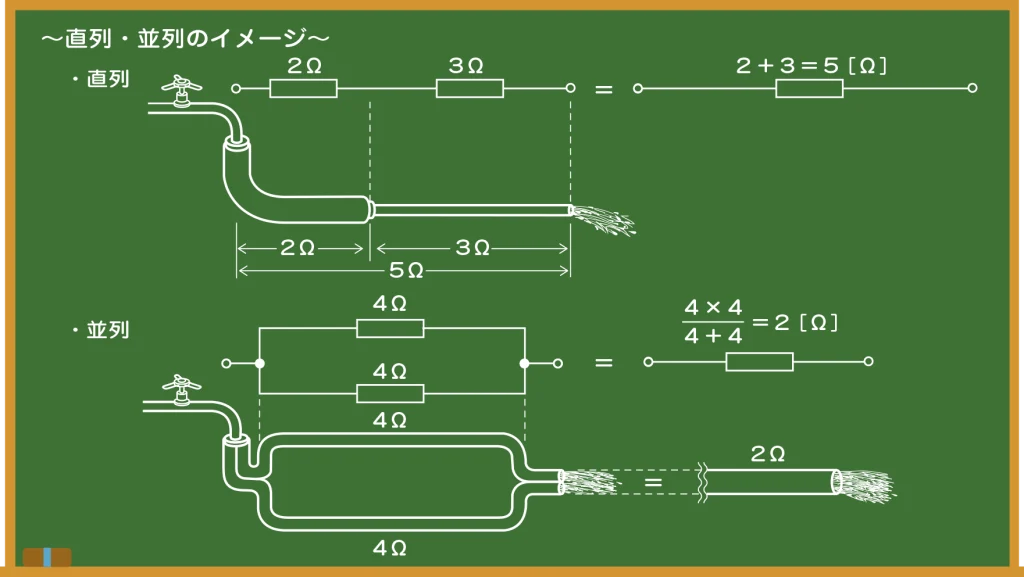
先生　抵抗のイメージを理解できたら、合成抵抗の計算もわかりやすくなるよ。
生徒　そうか、直列はホース同士をつなげると考えればいいんだ！
先生　そう。直列の合成抵抗がたし算というのも、これで納得できるでしょう？
生徒　並列はホースの本数が増えるから水（電流）が流れやすくなるんですね。
先生　そのイメージができればOKだよ。よし、次のステップに進もう。
生徒　はい！

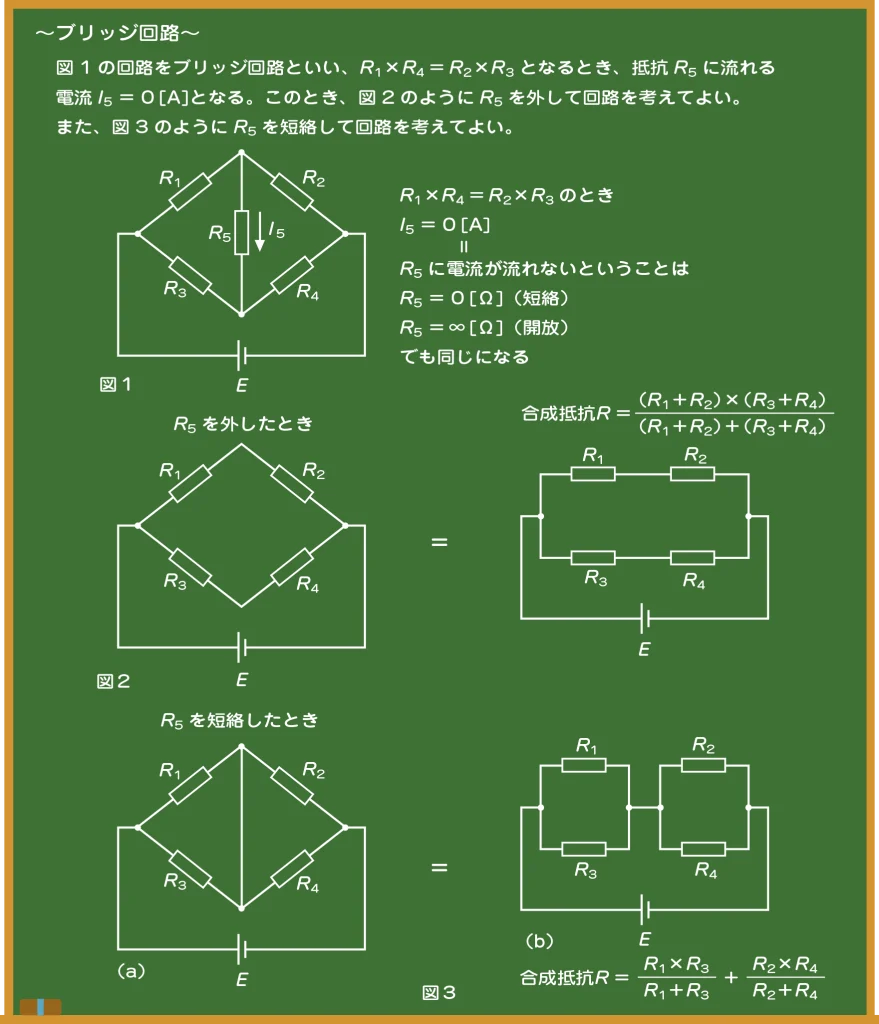
先生　それでは黒板に注目。このような回路を「ブリッジ回路」と呼ぶんだ。
生徒　難しそう……。
先生　そう思うよね。でも、この回路の抵抗で「R₁×R₄＝R₂×R₃」の関係が成り立つと、一気に簡単な回路になるよ。もちろん、成立しない場合もあるけど、ブリッジ回路が出てきたら、まずは「R₁×R₄＝R₂×R₃」が成り立つか調べるのが解答の鉄則になるんだ。
生徒　それにしても「R₁×R₄＝R₂×R₃」って、覚えにくいなぁ……。何かコツはありますか？
先生　向かい合う抵抗の積が等しいと覚えておけばいいよ。
生徒　あっ、ホントだ！
先生　それでは、練習問題に取り組んで今日は終わりにしよう。
生徒　はい、ありがとうございました！

練習問題
　次の回路における端子a－b間の合成抵抗R［Ω］を求めなさい。

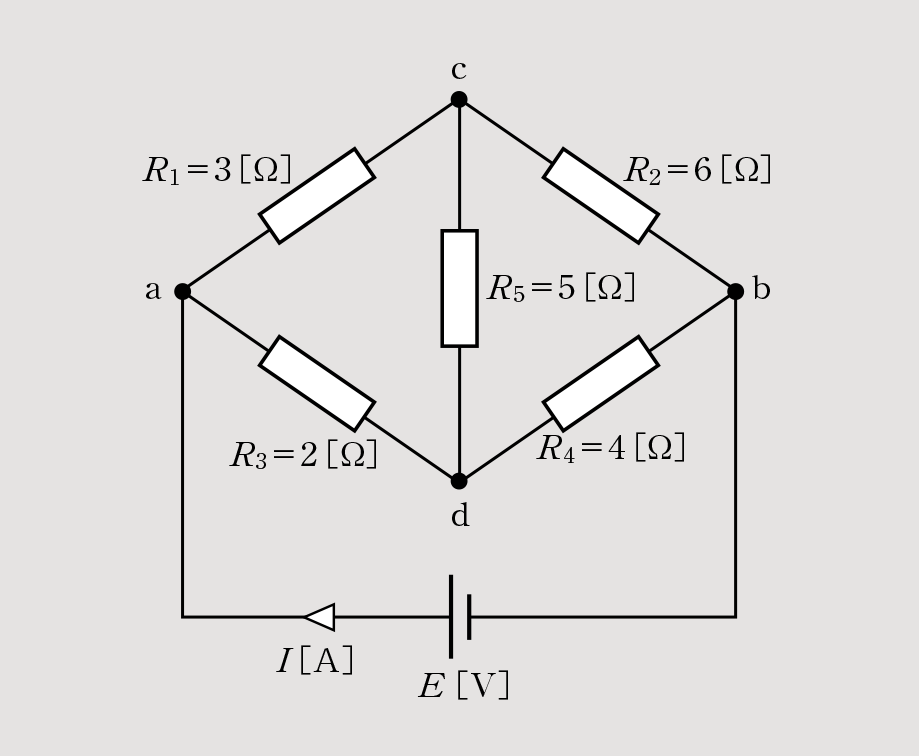
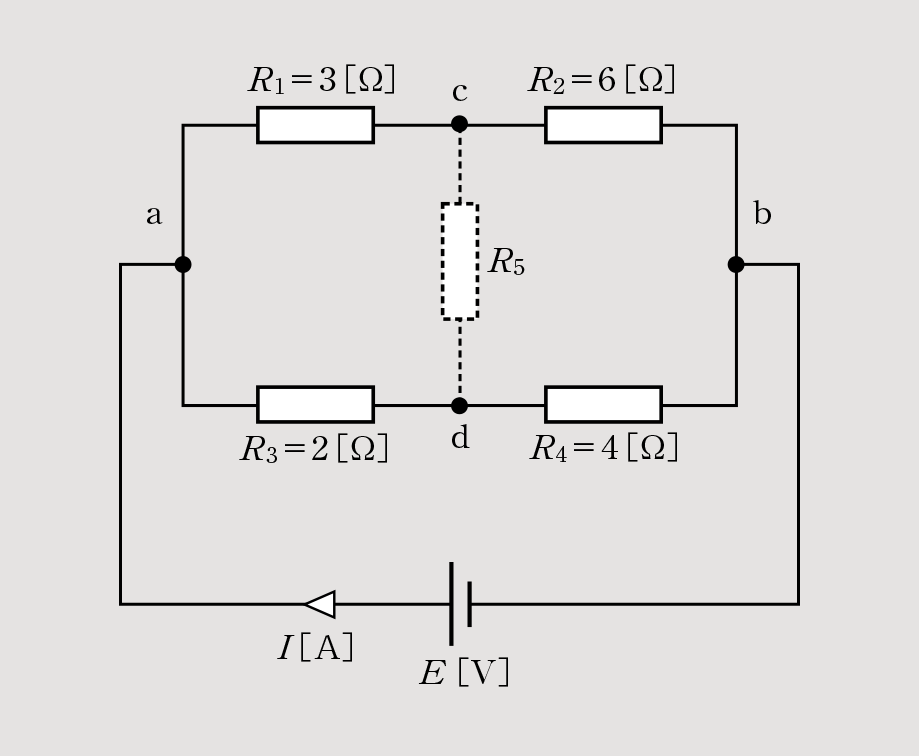
答
　このブリッジ回路が平衡しているか調べるため、まずは「R₁×R₄＝R₂×R₃」が成り立つか確認する。
　R₁×R₄＝3×4＝12
　R₂×R₃＝6×2＝12
　ここから「R₁×R₄＝R₂×R₃」が成り立つのでブリッジ回路は平衡状態であると判断できる。したがって、問題図は以下のような図になる。
　以上より、合成抵抗R［Ω］を求める。
　R₁₂＝R₁＋R₂＝3＋6＝9、R₃₄＝R₃＋R₄＝2＋4＝6
　R＝ $\frac{R_{12} \times R_{34}}{R_{12} + R_{34}}$ ＝ $\frac{9 \times 6}{9 + 6}$ ＝ $\frac{54}{15}$ ＝3.6［Ω］