電験取得のための分数の四則演算【電気数学のすゝめ2】

電験取得のための第一歩

2023.08.23

2限目　分数の四則演算

MathMagic Equation – www.mathmagic.com

先生　さて、今回は分数の四則演算に取り組んでみよう。分母の数が等しい分数のたし算とひき算は「分母はそのままで、分子だけ計算する」だよ。生徒　難しいような気がしたけど、やってみるとカンダンだ！先生　うん。そうしたら、たし算の例を下の図で考えてみよう。

\frac{3}{8}

と

\frac{1}{8}

を合わせると、円の半分になるのがわかるよね。

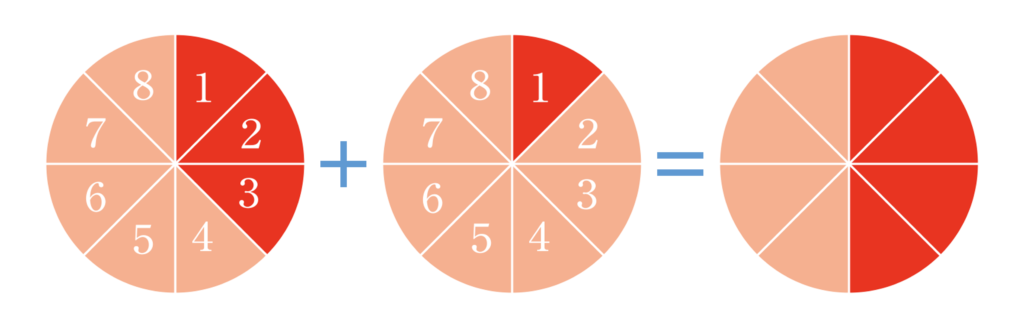
生徒　確かに、半分になっている。 $\frac{1}{2}$ と同じ！
先生　そう。そのまま計算すると $\frac{4}{8}$ になるけど、実は、 $\frac{1}{2}$ と同じことなんだ。このように、一番小さい数の分数に直すことを「約分」っていうんだ。
生徒　 $\frac{4}{8}$ より $\frac{1}{2}$ のほうがイメージしやすいですね。でも、頭のなかで円を考えて計算するのは時間がかかりますよね。何かいい方法はありませんか？
先生　そうだね。方法としては「分子と分母を0以外の同じ数でわる」といいよ。分数は分母と分子を0以外の同じ数でかけても、わっても、大きさは変わらないという性質があるからね。例えば、 $\frac{4}{8}$ の場合、分子と分母は「2」でわれそうだ。そうすると、 $\frac{4 \div 2}{8 \div 2}$ ＝ $\frac{2}{4}$ となるよね。
生徒　 $\frac{2}{4}$ なら、また2でわれそうです。 $\frac{2 \div 2}{4 \div 2}$ ＝ $\frac{1}{2}$ ですね。
先生　そう、そういうことだ！　それじゃあ、練習問題に取り組んで約分をマスターしよう。

練習問題
次の計算をしなさい。なお、約分できるものは約分すること。
（1） $\frac{1}{9} + \frac{2}{9}$ 　　（2） $\frac{11}{14} - \frac{9}{14}$ 　（3） $\frac{6}{10} - \frac{3}{10}$
（4） $\frac{17}{25} + \frac{2}{25}$ 　（5） $\frac{17}{33} - \frac{6}{33}$ 　（6） $\frac{27}{75} + \frac{8}{75}$
答
（1） $\frac{1}{9} + \frac{2}{9} = \frac{1 + 2}{9} = \frac{3}{9}$ （分子と分母を3でわる）＝ $\frac{1}{3}$
（2） $\frac{11}{14} - \frac{9}{14} = \frac{11 - 9}{14} = \frac{2}{14}$ （分子と分母を2でわる）＝ $\frac{1}{7}$
（3） $\frac{6}{10} - \frac{3}{10} = \frac{6 - 3}{10} = \frac{3}{10}$
（4） $\frac{17}{25} + \frac{2}{25} = \frac{17 + 2}{25} = \frac{19}{25}$
（5） $\frac{17}{33} - \frac{6}{33} = \frac{17 - 6}{33} = \frac{11}{33}$ （分子と分母を11でわる）＝ $\frac{1}{3}$
（6） $\frac{27}{75} + \frac{8}{75} = \frac{27 + 8}{75} = \frac{35}{75}$ （分子と分母を5でわる）＝ $\frac{7}{15}$

先生　約分もマスターしたようだね。よし、次のテーマに入ろう。「 $\frac{1}{2} + \frac{1}{5}$ ＝？」は解けるかな？
生徒　こんなのカンタンです！　分数のたし算だから、同じように……　あれ？　前の問題と違って分母が同じ数じゃない。どうやって計算すればいいんだろう。分子も分母も、そのままたせばいいのかな？
先生　その方法だとダメなんだ。まずは、分母を同じ数にそろえてあげるんだよ。お互いの分母の数をかけると、すぐに共通の数が出てくるね。

$\frac{1}{2} + \frac{1}{5} = \frac{1 \times 5}{2 \times 5} + \frac{1 \times 2}{5 \times 2} = \frac{5}{10} + \frac{2}{10} = \frac{7}{10}$

このように、分母を同じ数にすることを「通分」というんだ。ここで重要になるのが「分子と分母の両方に同じ数をかける」ということ。分子と分母に同じ数をかけないと、最初の分数の大きさが変わってしまうからね。さて、早速、トレーニングしてみよう。

練習問題
次の計算をしなさい。なお、約分できるものは約分すること。
（1） $\frac{1}{6} + \frac{1}{7}$ 　　（2） $\frac{1}{8} - \frac{1}{9}$ 　（3） $\frac{8}{14} - \frac{2}{7}$ 　(4） $\frac{6}{12} + \frac{5}{6}$
（5） $\frac{3}{10} - \frac{2}{5}$ 　　（6） $\frac{3}{13} + \frac{3}{4}$ 　（7） $\frac{3}{4} + \frac{5}{8}$ 　 (8） $\frac{5}{6} - \frac{3}{5}$
答
（1） $\frac{1}{6} + \frac{1}{7} = \frac{1 \times 7}{6 \times 7} + \frac{1 \times 6}{7 \times 6} = \frac{7}{42} + \frac{6}{42} = \frac{13}{42}$
（2） $\frac{1}{8} - \frac{1}{9} = \frac{1 \times 9}{8 \times 9} - \frac{1 \times 8}{9 \times 8} = \frac{9}{72} - \frac{8}{72} = \frac{1}{72}$
（3） $\frac{8}{14} - \frac{2}{7} = \frac{8 \times 7}{14 \times 7} - \frac{2 \times 14}{7 \times 14} = \frac{56}{98} - \frac{28}{98} = \frac{28}{98}$ （分子と分母を14でわる）＝ $\frac{2}{7}$
（4） $\frac{6}{12} + \frac{5}{6} = \frac{6 \times 6}{12 \times 6} + \frac{5 \times 12}{6 \times 12} = \frac{36}{72} + \frac{60}{72} = \frac{96}{72}$ （分子と分母を24でわる）＝ $\frac{4}{3}$
（5） $\frac{3}{10} - \frac{2}{5} = \frac{3 \times 5}{10 \times 5} - \frac{2 \times 10}{5 \times 10} = \frac{15}{50} - \frac{20}{50} = - \frac{5}{50}$ （分子と分母を5でわる）＝ $- \frac{1}{10}$
（6） $\frac{3}{13} + \frac{3}{4} = \frac{3 \times 4}{13 \times 4} + \frac{3 \times 13}{4 \times 13} = \frac{12}{52} + \frac{39}{52} = \frac{51}{52}$
（7） $\frac{3}{4} + \frac{5}{8} = \frac{3 \times 8}{4 \times 8} + \frac{5 \times 4}{8 \times 4} = \frac{24}{32} + \frac{20}{32} = \frac{44}{32}$ （分子と分母を4でわる）＝ $\frac{11}{8}$
（8） $\frac{5}{6} - \frac{3}{5} = \frac{5 \times 5}{6 \times 5} - \frac{3 \times 6}{5 \times 6} = \frac{25}{30} - \frac{18}{30} = \frac{7}{30}$

生徒　通分すると、分子も分母も数が大きくなるから、計算が大変でした。約分できるかどうかも考えないといけないし……。
先生　実は、もっと計算がラクになる通分の方法があるんだよ。
生徒　ホントですか？　教えてください！
先生　まずは、考えてみてよ。ヒントは約分できた計算問題のなかにあるんだ。
生徒　う～ん。
先生　例えば、練習問題（3）をみてみよう。分母の数で気がつくことはないかな？
生徒　あっ、14は7の倍数だ！
先生　いいところに気がついたね。そう、この問題で通分する場合、次のように分母を14で通分すれば計算がラクになるよ。

$\frac{8}{14} - \frac{2}{7} = \frac{8}{14} - \frac{2 \times 2}{7 \times 2} = \frac{8}{14} - \frac{4}{14} = \frac{4}{14} = \frac{2}{7}$

生徒　ずいぶんラクになりました。最初から教えてくれたらよかったのに……。
先生　ものごとは順序が大切なんだ。遠回りでも、試行錯誤して答えを導くほうが身につくんだよ。
生徒　は～い。
先生　実は、まだ計算をラクに行う方法があるんだ。次は $\frac{8}{14}$ に注目してみよう。何か気がつかない？
生徒　あっ、2で約分できます！
先生　正解！　だから、練習問題（3）は次のように解くこともできるね。計算する前に約分できるかどうかを確かめると、数字が大きくならないから計算がラクになるよ。

$\frac{8}{14} - \frac{2}{7} = \frac{4}{7} - \frac{2}{7} = \frac{2}{7}$

生徒　ほかの問題でも試してみよう。
先生　それが終わったら、今回の授業はここまでにしよう。
生徒　ありがとうございました。

別解
（4） $\frac{6}{12} + \frac{5}{6} = \frac{3}{6}$ （2で約分） $+ \frac{5}{6} = \frac{8}{6} = \frac{4}{3}$
（5） $\frac{3}{10} - \frac{2}{5} = \frac{3}{10} - \frac{2 \times 2}{5 \times 2} = \frac{3}{10} - \frac{4}{10} = - \frac{1}{10}$
（7） $\frac{3}{4} + \frac{5}{8} = \frac{3 \times 2}{4 \times 2} + \frac{5}{8} = \frac{6}{8} + \frac{5}{8} = \frac{11}{8}$

（講師／村山慎一）

電気数学のすゝめ記事一覧

技術者必携ライセンスの解答例を一挙公開！

License Special

第二種電気工事士

＞上期学科試験（筆記方式）
5月25日（日）解答速報！

コメントを残す

「OhmshaOnline」が不適切だと判断した場合、投稿の削除コメント機能の利用停止などの措置を行うことがあります。

電験取得のための分数の四則演算【電気数学のすゝめ2】

2限目 分数の四則演算

電気数学のすゝめ 記事一覧

License Special

2限目　分数の四則演算

電気数学のすゝめ記事一覧