License
小数、百分率、パーユニット法、パーセントインピーダンスを学ぶ【電気数学のすゝめ12】
電験取得のための第一歩
2024.09.24
12限目 さまざまな数値の表現
先生 前回まで、分数をメインに扱いたかったから、すべて解答は分数で表現していたんだけど、気づいたかな？
生徒 あっ、言われてみれば……。気づきませんでした。
先生 そうだよね（苦笑）。電験三種では、解答が小数や百分率などで表現されることもあるから、今回は分数から小数や百分率への変換に取り組んでみようか。
生徒 それは簡単ですよ。分子を分母で割れば小数になりますからね！
先生 それでは、練習問題を取り組んでみてよ。
練習問題
次の分数を小数で表しなさい。
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
答
（1）
=1÷4=0.25
（2）
＝2÷5＝0.4
（3）
＝3÷2＝1.5
（4）
＝7÷10＝0.7
（5）
＝52÷10＝5.2
（6）
＝21÷100＝0.21
（7）
＝2÷3＝0.6666……＝0.6
（8）
＝17÷11＝1.545454……＝1.54
生徒 はい、できました！ 余裕ですよ!!
先生 うん、正解だ。（6）までは暗算でできるといいね。
生徒 試験では電卓が使えるから、暗算ができなくてもいいんじゃないの？
先生 その認識は間違い！ 電卓は入力ミスのおそれもあるから、計算結果だけを信じ込むのはいけないことなんだ。だから、どんな値になるか、暗算で予想して計算することが大切なんだよ。
生徒 は～い、わかりました！
先生 ところで、（7）と（8）はできたかな。同じ数字が繰り返し現れる小数のことをなんていうかわかる？
生徒 循環小数、でしたっけ？
先生 うん、正解。電験三種では選択肢の値を参考に四捨五入して計算するんだよ。それじゃあ、次は百分率で数値を表してみよう。
生徒 百分率って、パーセント（％）のことですよね。よくデパートで「大特価セール、40％オフ！」という表示をみたことがあります。
先生 そう、それそれ！ 電験三種では効率、力率、すべりなどを表すときに使われているんだよ。ところで、40％を小数にすると、どうなる？
生徒 40÷100＝0.4ですよね。
先生 百分率は全体を100と考えたときの割合を表す値だから、百分率を小数で表すには100で割ればいいよね。それじゃあ、小数を百分率で表すには、どうすればいいかな？
生徒 100をかける！
先生 うん、そのとおり。
練習問題
（1）6％を小数で表しなさい。
（2）45％を小数で表しなさい。
（3）0.33を百分率［％］で表しなさい。
（4）1.05を百分率［％］で表しなさい。
答
（1）6［％］＝
＝0.06
（2）45［％］＝
＝0.45
（3）0.33＝0.33×100＝33［％］
（4）1.05＝1.05×100＝105［％］
先生 もうひとつ、百分率のほかにも覚えておきたい表記があるんだ。
生徒 ……。
先生 そんなイヤな顔をしないでよ。パーユニット法という表記で、百分率では「％」を使ったけど、パーユニット法では「p.u」という表記を使うんだ。
生徒 百分率と何が違うんですか？
先生 うん、いい質問だね。百分率は100を基準とするのに対して、パーユニット法は1を基準にしている値なんだよ。
生徒 う～ん、どういうこと？
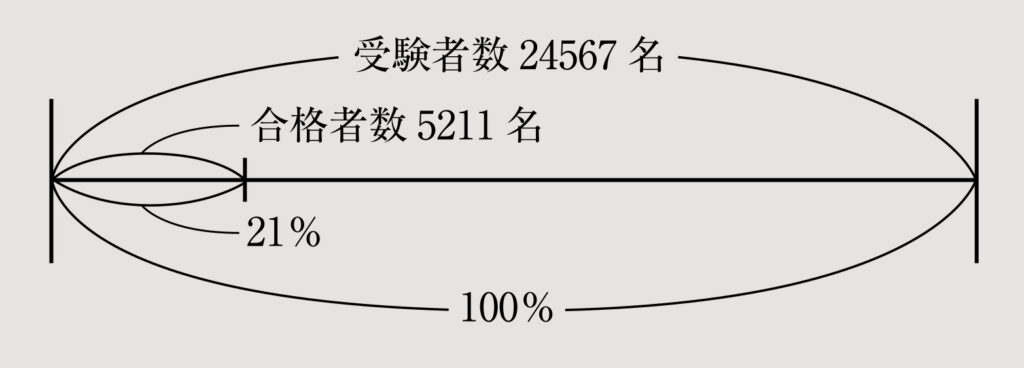
先生 例えば、令和5年度下期の電験三種（筆記方式）の受験者数は24567名、合格者数は5211名でした。この場合、合格率は何％かな？
生徒
だから、
≒0.21となって、百分率に変換すると0.21×100＝21［％］で、答は21％です！
先生 うん、正解。21％の合格率ということは、受験者が100名なら、21名しか合格できない試験ということ。このように、百分率で表記した値は100を基準に、どのくらいの割合かを表しているんだ。
生徒 これがパーユニット法だと？
先生 0.21p.u.という表記になるよ。
生徒 えっ、なんで??
先生 順を追って説明しようか。まず、百分率では100を基準にすると説明したね。電験三種の合格率の例では「24567名の受験者数を100％としたとき、5211名の合格者数は何％になりますか？」と変換できる。これを比で表すと「24567名：5211名＝100％：□％」となるよね。ここから「外項の積＝24567×□、内項の積＝5211×100」となって、外項の積＝内項の積だから、24567×□＝5211×100となり、
□＝
×100≒0.21×100＝21［％］
と求めることができるよね。
生徒 はい。
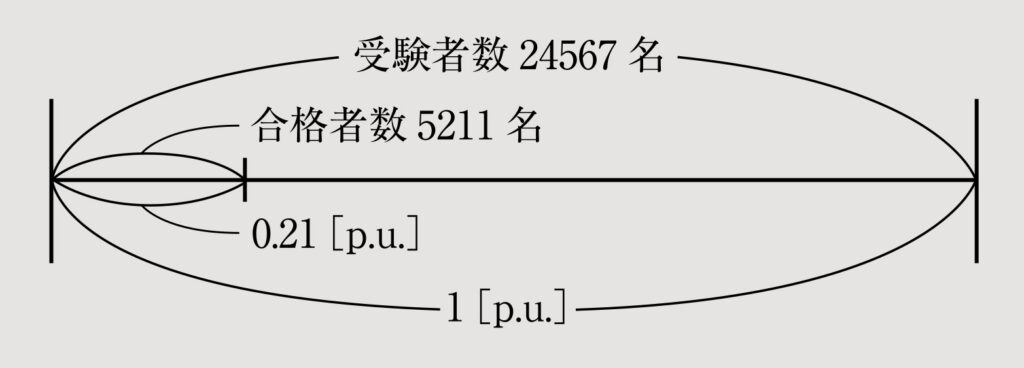
先生 パーユニット法でも同じように考えてみよう。パーユニット法では1を基準とするから、「24567名の受験者数を1p.u.としたとき、5211名の合格者数は何p.u.になりますか？」と変換することができるんだ。これを比で表すと「24567名：5211名＝1p.u.：□p.u.」となり、「外項の積＝24567×□、内項の積＝5211×1」から「外項の積＝内項の積」を利用して、24567×□＝5211×1、
□＝
≒0.21［p.u.］
と求めることができる。アバウトにいえば、百分率を小数に変換した値がパーユニット法の値になるんだ。
生徒 う～ん。電気の分野では、どのように使われているんでしょうか？
先生 具体的な問題をみてみようか。
「基準電圧を6.6kVとしたとき、3.3kVは何p.u.になるか求めなさい」
生徒 この場合、何を1p.u.に考えればいいんだ……。
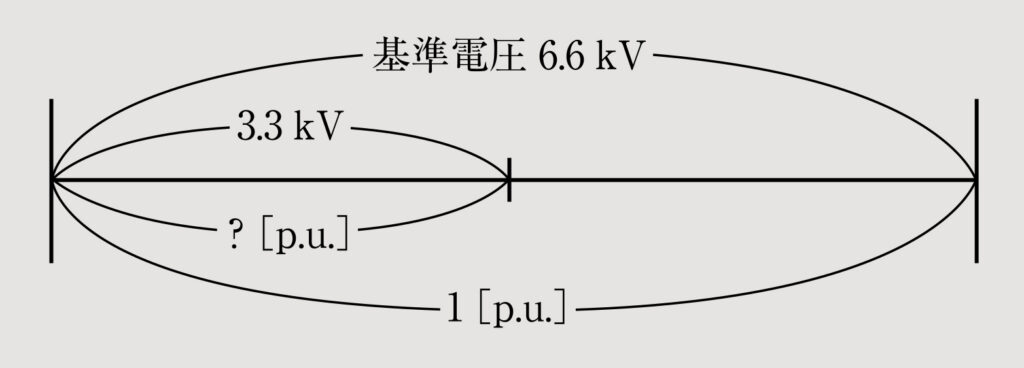
先生 まず、基準電圧である6.6kVを1p.u.と考えるんだ。このとき、3.3kVは何p.u.になるかだから、あとは比の計算で求められるよね？
生徒 はい！ 比で表すと「6.6kV：3.3kV＝1p.u.：□p.u.」となって、「外項の積＝6.6×□、内項の積＝3.3×1」から「外項の積＝内項の積」を利用して、6.6×□＝3.3×1、
□＝
＝0.5［p.u.］
となります！
先生 うん、正解だ！ それじゃあ、次の問題を取り組んでみようか。
「基準容量を10MV・Aとしたとき、20MV・Aは何p.u.になるか求めなさい」
生徒 10MV・Aを1p.u.としたときの20MV・Aを求めればいいから、比で考えると「10MV・A：20MV・A＝1p.u.：□p.u.」となって、「外項の積＝10×□、内項の積＝20×1」から「外項の積＝内項の積」を利用して、10×□＝20、
□＝
＝2［p.u.］です。
先生 うん、正解。ところで、この問題から「20MV・Aが2p.u.である」ことがわかったよね。実は、これに意味があるんだけど、説明できるかな？
生徒 計算方法はわかったけど、その意味までは……。
先生 この問題をわかりやすく変換すると「20MV・Aは10MV・Aの何倍ですか？」となるんだ。解答は2p.u.だから、20MV・Aは10MV・Aの2倍という意味になるんだよ。
生徒 最初から教えてくれればいいのに……。つまり、基準〇〇（基準値）の何倍なのかを考えればいいんですね。
先生 うん、そういうことだ。
生徒 それじゃあ、比を使わなくてもパーユニット法に変換したい値を基準値で割ればいいってことですよね？ 例えば、今回の問題なら
＝2［p.u.］と計算できます。
先生 そう、よく気づいたね。もちろん、それでもOKだよ。でも、どちらが分子で、どちらが分母か混乱してしまうこともあるから、比の計算は覚えておくといいね。それじゃあ、練習問題で確認しておこうか。
練習問題
（1）基準電圧を6.6kVとするとき、66kVは何p.u.か求めなさい。
（2）基準インピーダンスを4.36Ωとするとき、50Ωは何p.u.か求めなさい。
（3）20MV・Aをパーユニット法で表したところ2p.u.であった。基準容量は何MV・Aか求めなさい。
答
（1）6.6kV：66kV＝1p.u.：□p.u.
外項の積＝6.6×□、内項の積＝66×1＝66より、外項の積＝内項の積を利用すると、
6.6×□＝66
□＝
＝10［p.u.］
となる。
別解として「66kVは6.6kVの何倍か？」という問題に置き換えられることから、
＝10［p.u.］
と求めることができる。
答 10［p.u.］
（2）4.36Ω：50Ω＝1p.u.：□p.u.
外項の積＝4.36×□、内項の積＝50×1＝50より、外項の積＝内項の積を利用すると、
4.36×□＝50
□＝
≒11.47［p.u.］
となる。
別解として「50Ωは4.36Ωの何倍か？」という問題に置き換えられることから、
≒11.47［p.u.］
と求めることができる。
答 11.47［p.u.］
（3）基準容量［MV・A］を1p.u.としたとき、20MV・Aが2p.u.だから、比で表すと「基準容量MV・A：20MV・A＝1p.u.：2p.u.」となる。
外項の積＝基準容量×2、内項の積＝20×1＝20より、外項の積＝内項の積を利用すると、
基準容量×2＝20
基準容量＝
＝10［MV・A］
となる。
答 10［MV・A］
生徒 これも電験三種に関係しているんですよね？
先生 うん。ずいぶん鋭くなってきたね。これは百分率インピーダンス（パーセントインピーダンス）に関係してくるんだ。
生徒 パーセントインピーダンス？
先生 大まかに説明すると、インピーダンスの「p.u.値」を「％」で表記することなんだ。いまはパーセントインピーダンスという言葉があるという認識で十分だよ。
生徒 電験三種では、どんな形で出題されるんですか？
先生 せっかくだから、問題を解いてみようか。
「基準容量20MV・A、インピーダンスが0.2p.u.の発電機を、基準容量10MV・Aに換算したときのインピーダンスは何p.u.になるか求めなさい」
生徒 う～ん、どこから手をつけようか……。
先生 まず、基準容量が20MV・Aから10MV・Aに換算されていることに注目しよう。何倍になっているかな？
生徒 20MV・Aが10MV・Aになっているから、
＝0.5
倍です。
先生 次に、インピーダンスについて考えてみよう。インピーダンスのp.u.値は、実は、基準容量に比例するんだ。基準容量が0.5倍なら、インピーダンスのp.u.値も0.5倍になるんだよ。
生徒 それじゃあ、0.2p.u.×0.5＝0.1［p.u.］ということ？
先生 そう、正解だ！ 簡単でしょう。この場合も比で計算するとミスを防止できるよ。よし、もう１問、少し異なる問題にチャレンジしてみようか。
「送電線から電源側をみた電気的特性は、基準容量100MV・A、インピーダンスが0.05p.u.である。基準容量10MV・Aに換算したときのインピーダンスは何p.u.になるか求めなさい」
生徒 まず、基準容量が100MV・Aから10MV・Aに換算されているから、基準容量は
＝0.1倍です。
先生 うんうん。
生徒 インピーダンスのp.u.値も0.1倍になるから、0.05p.u.×0.1＝0.005［p.u.］と求めることができます。
先生 うん、正解。それじゃあ、比の計算を使ったら、どうやって求められる？
生徒 えっと、比で考えると「100MV・A：10MV・A＝0.05p.u.：□p.u.」となって、「外項の積＝100×□、内項の積＝10×0.05＝0.5」から「外項の積＝内項の積」を利用して、100×□＝0.5、□＝
＝0.005［p.u.］になります！
先生 うん、カンペキだ！
生徒 値が小さいから0の数に気をつけないといけませんね。
先生 だから、パーセントインピーダンスが登場するんだ。インピーダンスの「p.u.値」は小さくて扱いにくいから、「％」に変換して表記しようと決められたんだよ。さっきの問題ではインピーダンスのp.u.値が0.005だったけど、これを％で表記すると？
生徒 0.005×100＝0.5［％］です！
先生 そう、それがパーセントインピーダンスの値だよ。電験三種ではパーセントインピーダンスで出題されることが多いから、この表記に慣れておくといいね。
生徒 はい！
先生 それじゃあ、仕上げに練習問題を解いて今回は終わりにしよう。
生徒 ありがとうございました！
練習問題
（1）基準容量15MV・A、パーセントインピーダンス5％の変圧器がある。基準容量を10MV・Aに変換したとき、パーセントインピーダンスの値［％］を求めなさい。
（2）基準容量100MV・Aで変圧器一次側から電源側をみたパーセントインピーダンスが5％であった。基準容量を10MV・Aに変換したとき、パーセントインピーダンスの値［％］を求めなさい。
答
（1）基準容量とパーセントインピーダンスを比で表すと「15MV・A：10MV・A＝5％：□％」となる。
外項の積＝15×□、内項の積＝10×5＝50より、外項の積＝内項の積を利用すると、
15×□＝50
□＝
≒3.33［％］
となる。
答 3.33［％］
（2）基準容量とパーセントインピーダンスを比で表すと「100MV・A：10MV・A＝5％：□％」となる。
外項の積＝100×□、内項の積＝10×5＝50より、外項の積＝内項の積を利用すると、
100×□＝50
□＝
＝0.5［％］
となる。
答 0.5［％］
（講師／村山 慎一）